Nachdem wir uns im letzten Statistik-Blogbeitrag ausführlich mit dem bekanntesten statistischen Lagemaß – dem arithmetischen Mittel – befasst haben, wenden wir uns heute weiteren wichtigen Mittelwerten zu – angefangen mit dem sogenannten Median. Bei diesem handelt es sich ebenfalls um ein statistisches Lagemaß, welches – im Gegensatz zum arithmetischen Mittel – auch für ordinalskalierte Daten berechnet werden kann. Der Median ist als derjenige Wert definiert, der genau in der Mitte der geordneten Werte (und diese Ordnung von Werten setzt natürlich mindestens ordinalskalierte Daten voraus) einer Verteilung liegt. Da es bei einer ungeraden Anzahl von Werten tatsächlich ganz genau einen „mittigen“ Wert gibt, während bei einer geraden Anzahl von Werten dagegen zwei Werte in der Mitte der Verteilung liegen, existieren für die Berechnung des Median zwei Formeln.
Bei einer ungeraden Anzahl von Werten wird der mittlere Wert der geordneten Verteilung gewählt:

Bei einer geraden Anzahl von Werten wird das arithmetische Mittel der „mittigen“ Werte gebildet:
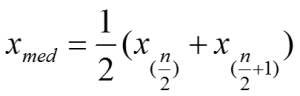
mit:
n = Anzahl der Werte der Verteilung
xn = Wert an n-ter Stelle der geordneten Verteilung
Robustheit des Median
Im Gegensatz zum arithmetischen Mittel ist der Median Ausreißern gegenüber äußerst robust. Dies zeigt sich am bereits bekannten Beispiel der Verteilungen [1; 2; 3; 4] und [1; 2; 3; 50]. Während das arithmetische Mittel der ersten Verteilung bei 2,5 liegt, liegt das Mittel bei der zweiten Verteilung bei 14 – dieses Lagemaß wird also durch den einzelnen, aus dem Rahmen fallenden Wert deutlich sichtbar nach oben verzerrt. Betrachtet man nun im Gegensatz dazu den Median, so ist festzustellen, dass dieser sowohl in der ersten als auch in der zweiten Verteilung bei 2,5 liegt – und somit durch den einzelnen Ausreißer überhaupt nicht beeinträchtigt wird.
Der Grund hierfür liegt auf der Hand: Während in die Berechnung des arithmetischen Mittels sämtliche Werte der Verteilung mit exakt dem gleichen Gewicht eingehen (also auch sämtliche Ausreißer), werden für die Berechnung des Median in diesem Fall lediglich zwei Werte (bei einer ungeraden Anzahl von Werten sogar lediglich ein Wert) benötigt, die in der Mitte der geordneten Verteilung liegen und daher unmöglich Ausreißer sein können. (Der Sonderfall einer Verteilung mit zwei Werten ist per se unsinnig und wird an dieser Stelle nicht weiter betrachtet.) Im Datensatz eventuell vorhandene Ausreißer gehen daher nicht in die Berechnung des Median ein – und können diesen somit auch nicht beeinflussen. Das Gedankenexperiment zeigt: Auch, wenn man in der zweiten Verteilung [1; 2; 3; 50] den Ausreißer auf 500, 5.000 oder 50.000 setzen würde, bliebe der Median stabil bei 2,5.
Perzentile
Im vorangegangenen Abschnitt haben wir die Definition des Median als den Wert kennengelernt, der exakt in der Mitte der geordneten Werte liegt. Diese Definition kann man abgewandelt auch wie folgt formulieren: 50% der Werte einer Verteilung sind entweder kleiner oder gleich dem Median, während die anderen 50% der Werte einer Verteilung entweder größer oder gleich dem Median sind. Diese Betrachtung macht deutlich, dass es sich beim Median lediglich um den Sonderfall eines anderen Lagemaßes – des Perzentils – handelt, der den Datensatz genau an der Marke 50/50 teilt. Ebenso sind aber natürlich auch noch andere Perzentile vorstellbar, die den Datensatz etwa an der Marke 20/80, 80/20, 45/55 oder 95/5 teilen. Der Median ist insofern lediglich das bekannteste – und meistberechnete – Perzentil. Gemeinsam mit dem 25%-Perzentil sowie dem 75%-Perzentil, bildet der Median die sogenannten Quartile, die einen Datensatz exakt in vier gleich große Wertebereiche unterteilen:
* 25%-Perzentil
(25% aller Werte liegen unterhalb dieses Wertes, 75% liegen oberhalb)
* 50%-Perzentil – Median
(50% aller Werte liegen unter- bzw. oberhalb dieses Wertes)
* 75%-Perzentil
(75% aller Werte liegen unterhalb dieses Wertes, 25% liegen oberhalb)
Anders formuliert handelt es sich bei dem 25%-Perzentil um den Median der Werte unterhalb des 50%-Perzentils, während das 75%-Perzentil den Median der Werte oberhalb des 50%-Perzentils darstellt. Die Differenz zwischen 75%-Perzentil und 25%-Perzentil spielt als sogenannter Interquartilsabstand (IQR = Inter Quartile Range) eine bedeutende Rolle bei der Konstruktion von Box-Plots und stellt zudem das einzige Streuungsmaß dar, das Ausreißern gegenüber robust ist.
Für die Berechnung beliebiger Perzentile existieren – analog zur Berechnung des Median – nun wiederum zwei Formeln. Ergibt die Multiplikation der gewünschten Perzentilgrenze p mit der Anzahl der Werte der Verteilung n (d.h. n * p), keinen ganzzahligen Wert, berechnet sich das Perzentil wie folgt:
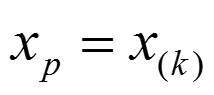
Dabei ist k die nächste auf das Ergebnis der Multiplikation (n * p) folgende, ganze Zahl. Ergibt (n * p) dagegen einen ganzzahligen Wert (in diesem Falle k), berechnet sich das Perzentil wie folgt:
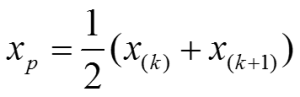
Modus
Der Modus – den wir der Kürze wegen an dieser Stelle noch an die Betrachtung des Medians anhängen wollen – ist das einzige Lagemaß, das auch für nominalskalierte Daten bestimmt werden kann. Er ist als der in den unklassierten Daten am häufigsten auftretende Wert definiert, bei gleichbreit klassierten Daten entspricht der Modus dagegen der Klassenmitte der Klasse, welche die meisten Werte auf sich vereinen kann. Der Modus lässt sich ohne Berechnung direkt aus den Daten herauslesen – allerdings nur dann, wenn ein eindeutiges Maximum (d.h. eine unimodale Verteilung) vorliegt. Bei bi- oder multimodalen Verteilungen kann der Modus in der Regel (es sei denn, zwei Werte treten tatsächlich exakt gleich oft auf) zwar rechnerisch bestimmt, jedoch nicht mehr sinnvoll interpretiert werden. Da keine scharfen Kriterien existieren, ist es der Anwenderin bzw. dem Anwender überlassen, wann eine Verteilung „gerade noch“ als unimodal gelten kann bzw. ab wann sie als bimodal gelten muss.
Auf eine Besonderheit bei der Verwendung von Software wie SPSS, PAST, SSP oder PSPP sei abschließend noch hingewiesen: Liegt ein bimodaler oder multimodaler Datensatz vor, wird zumeist nur der in der Häufigkeitstabelle zuoberst stehende, am häufigsten auftretende Wert als Modus ausgegeben. Dies ist dann selbstverständlich kein gültiger Modus – auch wenn SPSS das anders sieht…

Beispielrechnungen
Median, Perzentile und Modus
Für eine Gruppe von Studierenden liegt folgende Altersverteilung vor:
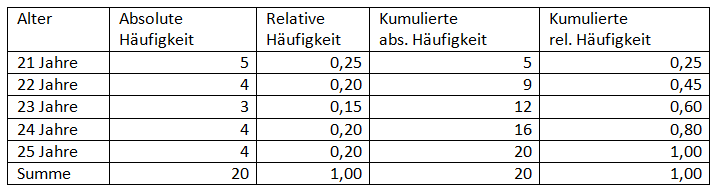
Um den Median berechnen zu können, müssen die Werte der Verteilung zunächst in eine geordnete Reihenfolge gebracht werden:
21; 21; 21; 21; 21; 22; 22; 22; 22; 23; 23; 23; 24; 24; 24; 24; 25; 25; 25; 25
Da es sich um eine gerade Anzahl an Werten handelt, steht kein einzelner Wert direkt in der Mitte der geordneten Verteilung. Für die Bestimmung des Median wird in diesem Fall daher auf die zweite Medianformel zurückgegriffen:
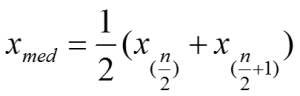
Es ist also das arithmetische Mittel des 10. (20/2) und des 11. (20/2+1) Wertes zu berechnen:
(23+23) / 2 = 23
Der Median liegt somit bei 23 Jahren.
Zusätzlich zum Median sollen nun noch das 25%-Perzentil sowie das 75%-Perzentil berechnet werden, um die Quartile vollständig angeben und den Interquartilsabstand bestimmen zu können. Hierzu wird wie folgt vorgegangen:
(0,25 * 20) = 5 -> ganzzahliger Wert -> k = 5
(0,75 * 20) = 15 -> ganzzahliger Wert -> k = 15
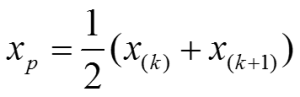
p0,25 = (x5 + x6) / 2 = (21+22) / 2 = 21,5
p0,75 = (x15 + x16) / 2 = (24+24) / 2 = 24
Die drei Quartile liegen demnach bei 21,5 Jahren (unteres Quartil), 23 Jahren (Median) und 24 Jahren (oberes Quartil), der IQR liegt bei 2,5 Jahren (24 – 21,5).
Da kein eindeutiges Maximum existiert, ist die Bestimmung des Modus in diesem Fall nicht angezeigt. Verwendet man zum Nachrechnen der Übungsaufgabe eine Statistiksoftware, wird diese dennoch eventuell 21 Jahre als Modus ausgeben. Dass dies kein sinnvolles Ergebnis ist, kann man sich hier aber sehr leicht vor Augen führen, indem man sich das Balkendiagramm der Verteilung anzeigen lässt – ein “eindeutiges Maximum” ist hier definitiv nicht gegeben.

Übungsaufgaben
Median und Quartile
Im Rahmen eines Lebensmittelprodukttests werden 25 Probandinnen und Probanden gebeten, den Geschmack eines neuen Joghurts auf einer Skala von 1 („hervorragend“) bis 5 („scheußlich“) zu bewerten. Der Test erbringt die folgenden Daten:

a) Bestimmen Sie den Median.
b) Bestimmen Sie den Interquartilsabstand.
Modus
Im Rahmen einer Qualitätsstichprobe werden 100 vom Band laufende Maschinenteile einer Kontrolle (Abweichung des Durchmessers von der zu erfüllenden Norm in mm) unterzogen. Die Stichprobenziehung erbringt die folgenden Daten.

a) Bestimmen Sie den Modus.
Zur Anzeige der Lösungen bitte hier klicken.
Die hier vorgestellten Inhalte und Aufgaben sind Teil der Vorlesung “Grundlagen der Statistik” im berufsbegleitenden Bachelor-Studiengang Betriebswirtschaftslehre an der Hochschule Harz. Eine vollständige Übersicht aller Inhalte dieser Vorlesung im Wissenschafts-Thurm findet sich hier: Grundlagen der Statistik.


Hallo,
ich habe eine Frage zur Perzentilberechnung. Wie ist die Formel mit n*p = ganzzahlig x_p = 1/2 ( x_k + x_(k+1) ) im Fall ordinalskalierter Daten zu verstehen? Hier taucht eine Summe auf, die aber nicht definiert ist. Gibt es in diesem Fall eine alternative Formel, die üblicherweise verwendet wird?
Konkretes Beispiel: Schulnoten von sechs Personen [1,1,2,3,3,6]. Median = 1/2 (2+3)?
Danke für den Blog. Er hilft mir gerade sehr und macht Spaß zu lesen :-).
Viele Grüße
Maik
@Maik: Vielen Dank für die Frage – wobei ich mir leider nicht sicher bin, ob ich sie korrekt verstanden habe. Ich versuche mich mal an einer Antwort – falls die aber nicht zufriedenstellend sein sollte, bitte einfach nochmal per Kommentar melden.
Der Median ist derjenige Wert, der genau in der Mitte der geordneten Verteilung liegt. Nehmen wir an, uns lägen die Schulnoten von fünf Personen vor:
[2, 3, 6, 1, 1]
Diese Werte können wir leicht in eine geordnete Reihenfolge bringen:
[1, 1, 2, 3, 6]
In diesem Fall ist der Median einfach zu erkennen, da ein Wert – nämlich die 2 – tatsächlich genau in der Mitte dieser geordneten Verteilung liegt. Kommt – wie im Beispiel im Kommentar – noch ein weiterer Wert hinzu, liegt kein einzelner Wert mehr in der Mitte der geordneten Verteilung:
[1, 1, 2, 3, 3, 6]
In diesem Fall bildet man das arithmetische Mittel aus den beiden in der Mitte liegenden Werten, d.h. (2+3) / 2 = 2,5. Auf die Formel übertragen, ergibt sich bei der Kalkulation von n * p (6 * 0,5) ein ganzzahliger Wert (k = 3), weshalb das arithmetische Mittel aus den beiden Werten an der k-ten (2) und der (k+1)-ten (3) Stelle der geordneten Verteilung zu bilden ist.
@Christian Danke, dass du das Beispiel ausführlich besprochen hast. Ich glaube, meine Frage ist noch nicht ganz beantwortet. Ich versuche sie nochmal anders zu formulieren:
Im Blog steht unter “arithmetisches Mittel”:
“Seine [die des arithmetischen Mittels] Berechnung setzt voraus, dass die Daten der Verteilung mindestens metrisch skaliert sind – was in der Praxis (etwa bei Schulnoten) bedauerlicherweise häufig übersehen wird.”
Gleichzeitig gilt bei diesem Beispiel:
“In diesem Fall bildet man das arithmetische Mittel aus den beiden in der Mitte liegenden Werten, d.h. (2+3) / 2 = 2,5.”
Für mich sieht das aus wie ein Widerspruch. Warum ist es korrekt bei der Berechnung des Medians ein arithmetisches Mittel von Daten zu bilden, die nicht metrisch skaliert sind?
@Maik: Ja, in dieser Vorgehensweise steckt in der Tat ein scheinbarer Widerspruch, den ich vermutlich leider auch nicht befriedigend aufklären können werde. In der Theorie berechnet man bei der Bestimmung des Medians aus einer geraden Anzahl an Werten nicht das arithmetische Mittel aus den beiden mittleren Werten, sondern das arithmetische Mittel aus zwei Lagemaßen, die man zuvor bestimmt hat – nämlich dem Obermedian und dem Untermedian (bei denen es sich natürlich aber um genau die beiden mittleren Werte handelt, insofern führt die beispielhafte Rechnung zum korrekten Ergebnis). Da Obermedian und Untermedian per Definition metrisch skalierte Kenngrößen sind, darf man aus Ihnen ein arithmetisches Mittel berechnen – auch wenn man es aus den beiden gleichen Zahlenwerten nicht hätte berechnen dürfen, sofern man diese als Elemente einer ordinal skalierten Verteilung betrachtet. Soweit zumindest mein Kenntnisstand – die wortexakte Begründung der Zulässigkeit dieses rechnerischenVorgehens müsste ich auch erst mal nachschlagen…
@Christian: Vielen Dank für den Hinweis mit dem Obermedian und Untermedian. Ich habe nochmal ein wenig für den Fall einer geraden Anzahl von Werten recherchiert: Wenn man den Median m als einen Wert definiert, bei dem die Hälfte der Stichprobenelemente =m ist, dann sind sowohl Obermedian, als auch Untermedian und alle möglichen Werte dazwischen ein Median. Diese Definition kann problemlos für ordinalskalierte Daten übernommen werden.
Im Fall von Schulnoten würden, wenn man davon ausgeht, dass es halbe und Viertelnoten gibt für das Beispiel [1, 1, 2, 3, 3, 6] die Noten [2, 2+, 2.5, 3-, 3] der oberen Definition eines Medians genügen.
Wenn es keine Viertelnoten gibt blieben nur noch [2, 2.5, 3] und wenn es keine halben Noten gibt nur noch [2, 3].