Was sind Rangkorrelationskoeffizienten?
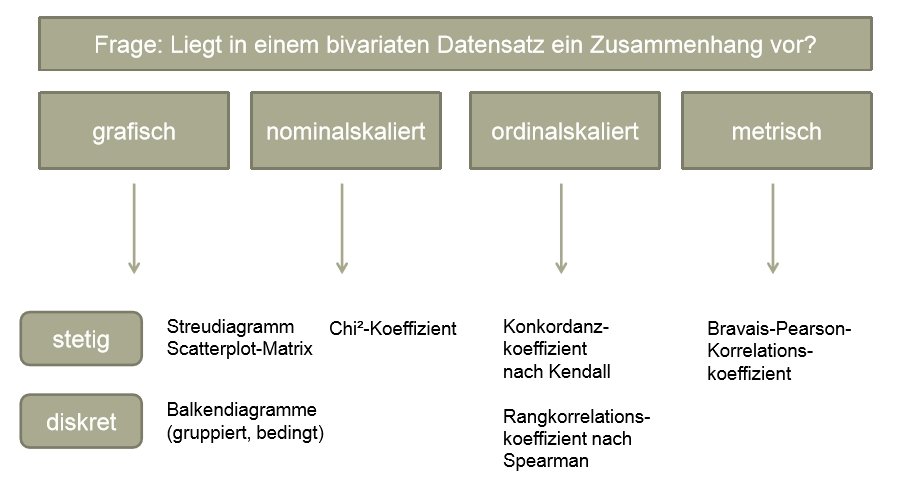
Liegen keine metrisch skalierten Daten vor, ist die Berechnung des Bravais-Pearson-Korrelationskoeffizienten (welcher zudem einen linearen Zusammenhang voraussetzt) nicht möglich. In diesem Fall (sowie auch in Fällen, in denen in metrischen Daten kein linearer Zusammenhang zu vermuten ist), können alternativ der Rangkorrelationskoeffizient nach Spearman sowie der Konkordanzkoeffizient nach Kendall berechnet werden.
Beide setzen lediglich ordinalskalierte Daten voraus und geben die Stärke des monotonen Zusammenhangs zwischen zwei Variablen wieder, wobei in gleichsinnige (große Werte einer Variablen gehen tendenziell mit großen Werten der anderen Variablen einher) und gegensinnige (große Werte einer Variablen gehen tendenziell mit kleinen Werten der anderen Variablen – und umgekehrt – einher) zu unterscheiden ist. Liegt ein linearer Zusammenhang vor, existiert stets auch ein monotoner Zusammenhang – umgekehrt kann aber durchaus ein monotoner Zusammenhang vorliegen, ohne dass auch ein linearer Zusammenhang existiert.
Der Grundgedanke hinter beiden Koeffizienten beruht auf dem Umstand, dass sich sowohl ordinale als auch metrische Daten in eine natürliche Reihenfolge bringen, d.h. ordnen lassen. Untersucht man den Grad der Korrelation zwischen zwei Reihen solcher Daten, kann man somit eine der Datenreihen ordnen und anschließend prüfen, inwiefern sich die zweite Datenreihe „mitgeordnet“ hat.
Liegt ein perfekter gleichsinniger Zusammenhang vor, so ist zu erwarten, dass sich die zweite Datenreihe auch perfekt mitordnet, d.h. (je nach gewählter Sortierung) entweder vom kleinsten zum größten oder vom größten zum kleinsten Datensatz. Im Falle eines perfekt gegensinnigen Zusammenhangs wäre dagegen zu erwarten, dass sich die zweite Datenreihe exakt entgegengesetzt zur ersten Datenreihe sortiert. Alle anderen Fälle weichen mehr oder weniger stark von diesen beiden Sonderfällen ab.
Mit den Koeffizienten nach Spearman und Kendall werden wir nachfolgend zwei Wege kennenlernen, mit denen wir den Grad der Abweichung in der Mitsortierung der zweiten Datenreihe von den beiden Sonderfällen der perfekten gleichsinnigen und der perfekten gegensinnigen Korrelation auf verschiedene Arten ermitteln und in einer leicht interpretierbaren Kennzahl ausdrücken können.
Der Rangkorrelationskoeffizient nach Spearman
Zur Bestimmung des Rangkorrelationskoeffizienten nach Spearman werden beide Datenreihen der Größe nach mit Rängen beziffert. Über die Summe der – bei Vorliegen eines perfekten gleichsinnigen Zusammenhangs nicht vorhandenen – quadrierten Differenzen zwischen den Rängen der ersten und der zweiten Datenreihe wird anschließend der Korrelationskoeffizient wie folgt berechnet:
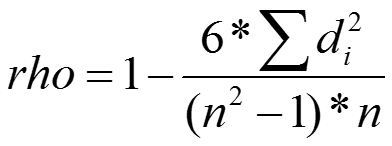
Die Vorgehensweise lässt sich am schnellsten anhand eines einfachen Beispiels erschließen:

Als Summe der quadrierten Rangdifferenzen ergibt sich hier also 6. Eingesetzt in die Formel für den Rangkorrelationskoeffizienten nach Spearman (gemeinsam mit n = 5) ergibt sich folgender Wert:
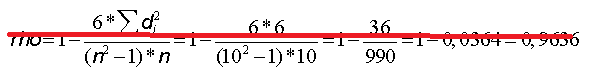
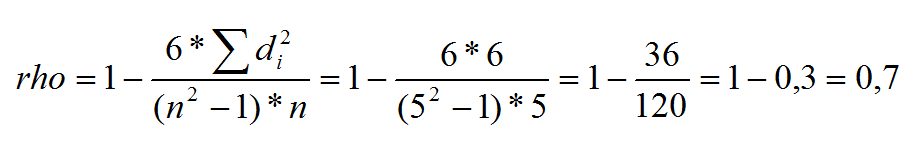
(Mit Dank an Jürgen Sporenberg für den Fehlerhinweis in den Kommentaren.)
Der Wert für „Spearmans Rho“ liegt stets zwischen -1 und +1 und ist wie folgt zu interpretieren:
- > 0 -> gleichsinniger monotoner Zusammenhang
- ≈ 0 -> kein monotoner Zusammenhang
- < 0 -> gegensinniger monotoner Zusammenhang
Ein Problem für die Aussagekraft des Koeffizienten stellt das Auftreten sogenannter verbundener Ränge (auch Rangplatzbindungen oder ties) dar: Treten Werte mehrfach auf, bekommen diese nämlich einen Durchschnittsrang (berechnet als arithmetisches Mittel der zu vergebenden Ränge) zugewiesen.

Je mehr verbundene Ränge nun aber existieren, umso geringer ist die Aussagekraft des Rangkorrelationskoeffizienten. Eine allgemeingültige Regel, ab welchem Anteil von verbundenen Rängen der Koeffizient nicht mehr berechnet werden sollte, existiert allerdings nicht, d.h. es bleibt eine subjektive Entscheidung. Eine Konstellation wie im obigen Beispiel dürfte allerdings in jedem Fall inakzeptabel sein.
Der Konkordanzkoeffizient nach Kendall
Auf dem gleichen Prinzip wie der Rangkorrelationskoeffizient nach Spearman basiert auch der Konkordanzkoeffizient nach Kendall. Für dessen Berechnung müssen daher ebenfalls zunächst die Ränge beider Variablenreihen gebildet werden. Anschließend werden die Daten nach den Rängen einer der beiden Datenreihen geordnet und wiederum überprüft, inwieweit sich die zweite Datenreihe „mitsortiert“ hat. Diese Überprüfung erfolgt anhand des paarweisen Vergleichs der Ränge der zweiten Datenreihe, wobei in konkordante (die natürliche Reihenfolge der Ränge wird eingehalten) und diskordante Paare (die natürliche Reihenfolge der Ränge wird nicht eingehalten) unterschieden wird.
Auch dieses Prinzip lässt sich am besten anhand des bereits bekannten Beispiels illustrieren:

In der ersten Zeile wird hier der y-Rang (1) mit den folgenden Rängen (2,4,5,3) verglichen. Dabei zeigt sich, dass auf die (1) nur größere Ränge folgen, die natürliche Ordnung also bei allen vier Paarvergleichen eingehalten wird. Für diese Zeile sind somit 4 konkordante und 0 diskordante Paare zu notieren.
Eine erste Abweichung zeigt sich in der dritten Zeile. Der Rang (4) ist hier mit den Rängen (5,3) zu vergleichen, wobei nur ein Paarvergleich konkordant (4<5), der andere jedoch diskordant (4>3) ausfällt. Insgesamt ergeben sich 8 konkordante (K) und 2 diskordante (D) Paare, die neben n (hier: 5) in die Formel für den Konkordanzkoeffizienten nach Kendall einzusetzen sind:
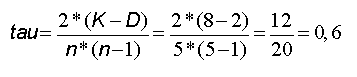
Wie beim Rangkorrelationskoeffizienten nach Spearman ergibt sich auch hier ein Wert zwischen -1 und +1, der analog zu interpretieren ist. Obwohl beide Koeffizienten auf dem gleichen Prinzip des „Ordnens und Mitordnens“ basieren, fließen in den Konkordanzkoeffizienten nach Kendall weitaus mehr Informationen ein, da nicht nur einzelne Rangpaare (über die Differenzen), sondern alle Ränge miteinander abgeglichen werden (über die Ermittlung der konkordanten und diskordanten Paare).
Ein Problem ergibt sich auch bei der Berechnung von Kendall durch verbundene Ränge, die in Paarvergleichen nicht mitgezählt werden. Im nachfolgenden, bereits bekannten Beispiel, ergeben sich im Rahmen von 10 Paarvergleichen nur 6 Werte, da ganze 4 Paarvergleiche mit identischen Werten ausscheiden.

Korrelation und Kausalität
Zur korrekten inhaltlichen Interpretation von Korrelationen wurde in einem der vorigen Blogposts bereits einiges geschrieben, das auch für die Interpretation des Rangkorrelationskoeffizienten nach Spearman sowie des Konkordanzkoeffizienten nach Kendall Gültigkeit besitzt und bei der Bearbeitung entsprechender Aufgaben beachtet werden sollte.
Beispielrechnungen
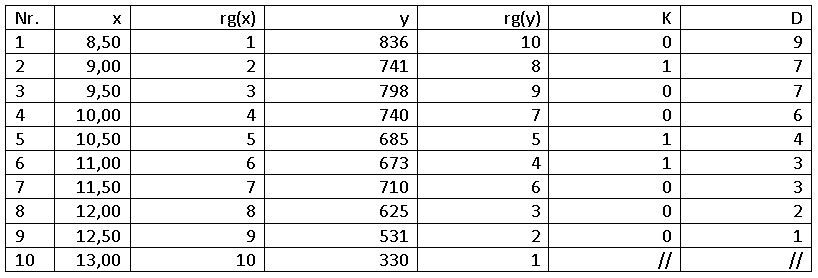
Ein Kinobetreiber verändert (ceteris paribus) über einen Zeitraum von 10 Tagen die Eintrittspreise für den Abendfilm und zeichnet die Besucherzahlen auf. Es ergibt sich die folgende Tabelle:
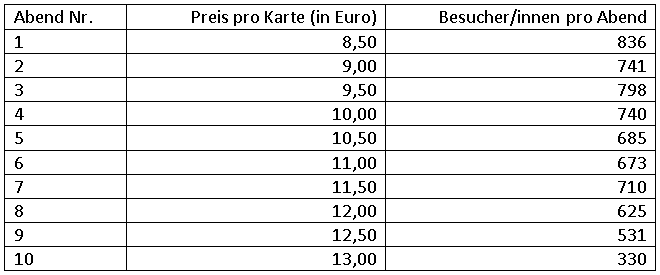
Bestimmung des Rangkorrelationskoeffizienten nach Spearman
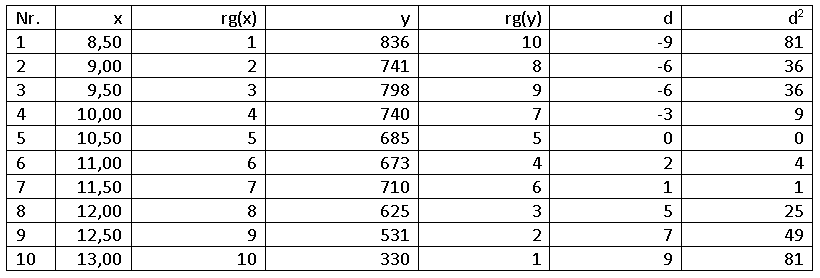
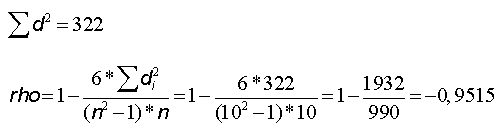
Bestimmung des Konkordanzkoeffizienten nach Kendall
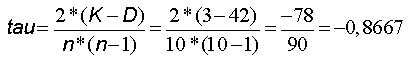
Übungsaufgaben
Die Wiederholung des Kinopreis-Experiments in einem anderen Kino über die Dauer von 5 Tagen erbrachte folgende Ergebnisse:
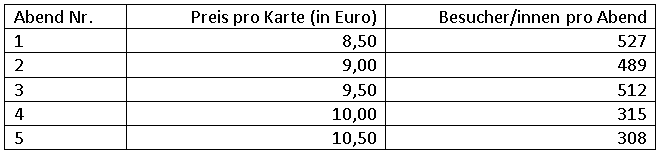
a) Berechnen Sie den Rangkorrelationskoeffizienten nach Spearman.
b) Berechnen Sie den Konkordanzkoeffizienten nach Kendall.
Zur Anzeige der Lösungen bitte hier klicken.
Die hier vorgestellten Inhalte und Aufgaben sind Teil der Vorlesung “Grundlagen der Statistik” im berufsbegleitenden Bachelor-Studiengang Betriebswirtschaftslehre an der Hochschule Harz. Eine vollständige Übersicht aller Inhalte dieser Vorlesung im Wissenschafts-Thurm findet sich hier: Grundlagen der Statistik.


Hallo,
ist im obrigen Beispiel nicht ein Rechenfehler?
Es geht um das Fallbeispiel für die Formel 1- (6x (Sigma d^1) ) / (n^2-1)*n
In der Tabelle sind 5 Werte, also n=5, in dem Beispiel wird aber n=10 gerechnet. Folglich kommt ein falsches Ergebnis raus, oder?
@Jürgen Sporenberg: Richtig! Das eigentliche Ergebnis liegt bei 0,7 statt bei 0,9 und damit deutlich dichter am Kendallschen Konkordanzkoeffizienten – die Größe dieser Differenz hätte mir eigentlich auffallen müssen. Ist (natürlich mit Dank an den Hinweisgeber) weiter oben im Beitrag korrigiert. Vielen Dank für den Hinweis!
Hallo,
ich hätte eine Frage ist Spearman anwendbar für eine Korrelation zwischen einer ordinalen Variable und einer binären Variable (ja, nein)?
Danke!
@Mohamed Fliss: Endlich mal eine Frage, zu der ich eine klare Auskunft geben kann: Leider nein. Zwar könnte man eine binäre Variable unter bestimmten Umständen (z.B. bei den Ausprägungen “größer x” und “kleiner x”) ggf. sogar noch als ordinalskaliert betrachten (ja/nein wäre es definitiv nicht und würde damit ohnehin ausscheiden) – letztlich würde der Versuch aber in der praktischen Umsetzung scheitern: Da man bei einer binären Variable mit einer Vielzahl verbundener Ränge zu rechnen hätte und Rangplatzbindungen die Aussagekraft sowohl von Spearman als auch von Kendall schwächen, würde sich die Berechnung keines der Koeffizienten lohnen.