(Der Blog-Beitrag zu dieser Übung findet sich hier.)
Spannweite, Interquartilsabstand und Fünf-Werte-Zusammenfassung
Gegeben seien die Angaben für das Alter von 30 befragten Personen.
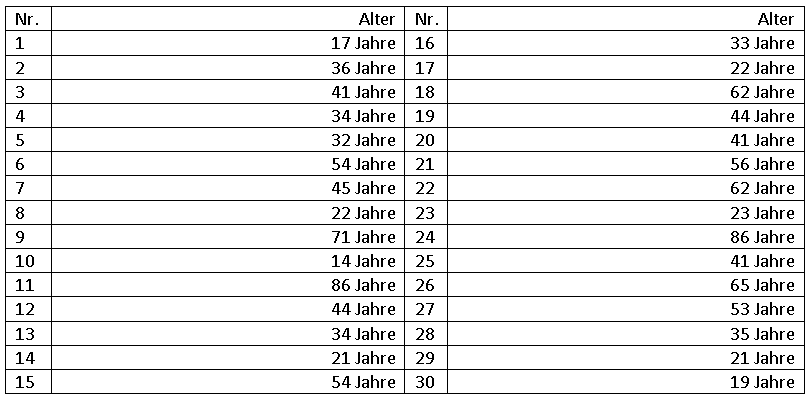
a) Bestimmen Sie die Spannweite.
b) Bestimmen Sie den Interquartilsabstand.
c) Bestimmen Sie die Fünf-Werte-Zusammenfassung.
Lösungen der Übungsaufgaben
Spannweite, Interquartilsabstand und Fünf-Werte-Zusammenfassung
a) Bestimmen Sie die Spannweite.
Die Spannweite ist definiert als Differenz zwischen dem größten und dem kleinsten Wert.
ds = xmax – xmin = 86 – 14 = 72
Die Spannweite beträgt 72 Jahre.
b) Bestimmen Sie den Interquartilsabstand.
Zur Bestimmung des IQR sind das obere sowie das untere Quartil zu berechnen. Hierfür müssen die Werte zunächst in eine geordnete Reihenfolge gebracht werden:
Wert 1-10: 14; 17; 19; 21; 21; 22; 22; 23; 32; 33
Wert 11-20: 34; 34; 35; 36; 41; 41; 41; 44; 44; 45
Wert 21-30: 53; 54; 54; 56; 62; 62; 65; 71; 86; 86
(30 * 0,25) = 7,5 -> kein ganzzahliger Wert -> k = 8 -> Der 8. Wert im Datensatz lautet 23
(30 * 0,75) = 22,5 -> kein ganzzahliger Wert -> k = 23 -> Der 23. Wert im Datensatz lautet 54
IQR = 54 – 23 = 31
Der Interquartilsabstand beträgt 31 Jahre.
c) Bestimmen Sie die Fünf-Werte-Zusammenfassung.
Die Fünf-Werte-Zusammenfassung umfasst die drei Quartile sowie den größten und den kleinsten Wert. Lediglich der Median als mittleres Quartil muss an dieser Stelle noch berechnet werden.
(30 * 0,50) = 15 -> ganzzahliger Wert -> k = 15; k+1 = 16 -> ½* (41 + 41) = 41
Die Fünf-Werte-Zusammenfassung lautet demnach:
[14 Jahre; 23 Jahre; 41 Jahre; 54 Jahre; 86 Jahre]
Die hier vorgestellten Inhalte und Aufgaben sind Teil der Vorlesung “Grundlagen der Statistik” im berufsbegleitenden Bachelor-Studiengang Betriebswirtschaftslehre an der Hochschule Harz. Eine vollständige Übersicht aller Inhalte dieser Vorlesung im Wissenschafts-Thurm findet sich hier: Grundlagen der Statistik.
