In unserem heutigen statistischen Grundlagenartikel soll es um die sogenannten Dispersionsparameter bzw. statistischen Streuungsmaße gehen. Diese geben Auskunft darüber, wie die Werte einer Verteilung um deren Zentrum (gekennzeichnet durch ein statistisches Lagemaß) streuen, d.h. ob sie tendenziell eher dicht am Zentrum oder eher weit von diesem entfernt liegen. Warum die Kenntnis dieser Streuung unter anderem für den Vergleich zweier Verteilungen von großer Bedeutung ist, soll das folgende fiktive Beispiel der Einkommensverteilung in zwei Abteilungen des gleichen Unternehmens mit je sechs Mitarbeiterinnen und Mitarbeitern verdeutlichen.
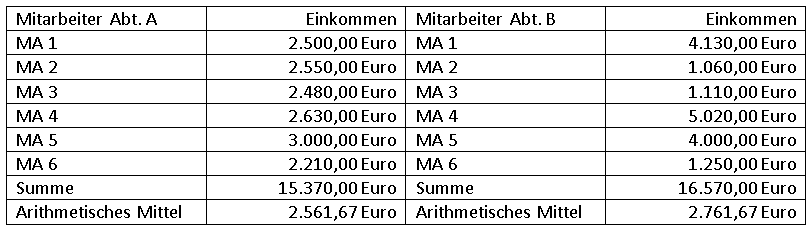
Wie man sieht, liegen die arithmetischen Mittel beider Verteilungen mit 2.561 Euro in Abteilung A und 2.761 Euro in Abteilung B gerade einmal 200 Euro voneinander entfernt – dennoch wäre es mit Blick auf die Daten falsch, würde man aus dieser geringen Differenz den Schluss ziehen, dass Mitarbeiterinnen und Mitarbeiter in beiden Abteilungen ungefähr gleich viel verdienen. Würde man nämlich in Abteilung A anheuern, könnte man in der Tat davon ausgehen, um 2.561 Euro zu verdienen. In Abteilung B liegt dagegen kein Mitarbeiter mit seinem Einkommen auch nur in der Nähe des Durchschnitts – hier verdient man entweder deutlich mehr oder deutlich weniger als 2.761 Euro.
Das Beispiel zeigt, dass es bei der Betrachtung von Verteilungen eben nicht nur darauf ankommt, das Zentrum einer Verteilung zu kennen – vielmehr muss man auch eine Vorstellung davon haben, wie sich die Werte um dieses Zentrum herum verteilen. Auskunft hierüber geben die Dispersionsparameter, von denen wir im Rahmen dieser Blogserie Spannweite, Interquartilsabstand, Varianz und Standardabweichung kennenlernen werden. Im heutigen Beitrag werden wir – neben der Theorie – zunächst die beiden „einfacheren“ Parameter Spannweite und Interquartilsabstand abarbeiten, während wir uns im nächsten Artikel dann der Varianz sowie der Standardabweichung zuwenden werden.
Dispersionsparameter und Skalenniveaus
Ähnlich wie schon bei den statistischen Lagemaßen, hängt auch die Wahl geeigneter Dispersionsparameter primär vom Skalenniveau der betrachteten Verteilung ab, wobei in diesem Fall nur zwei Skalenniveaus – Ordinal- und Kardinalskala – von Bedeutung sind. Da nominalskalierte Werte nicht quantifiziert werden können, können sie auch nicht um das Zentrum einer Verteilung (in diesem Fall also um den Modus) streuen, weil das Vorhandensein einer Streuung natürlich voraussetzt, dass sich die Abstände zwischen den Werten einer Verteilung und ihrem Zentrum ermitteln lassen. Da dies bei nominalskalierten Werten nicht möglich ist, existiert kein Maß für deren Streuung. Man kann sich das leicht vor Augen führen, indem man etwa mit dem Geschlecht ein beispielhaftes nominalskaliertes Merkmal betrachtet: Befragt man 40 Personen, von denen 30 männlich sind, ist „männlich“ zwar der Modus – aber wie sollte in diesem Fall eine „Streuung“ der Werte um dieses Zentrum aussehen?
Die Berechnung des Interquartilsabstands verlangt mindestens ordinalskalierte Werte, da – wie wir nachfolgend noch sehen werden – das obere und untere Quartil in diesen Parameter einfließen, deren Berechnung ja ebenfalls ordinaskalierte Werte voraussetzt. Da in die Berechnung der Varianz sowie der sich aus der Varianz ergebenden Standardabweichung das arithmetische Mittel einfließt, können diese beiden Parameter analog nur für metrisch skalierte Werte berechnet werden. Auch die Berechnung der Spannweite ist – aus Gründen, die wir nachfolgend noch betrachten werden – nur für metrisch skalierte Werte sinnvoll. Wie bei den statistischen Lagemaßen gilt auch für die Dispersionsparameter, dass sie abwärts-, aber nicht aufwärtskompatibel sind, d.h. der Interquartilsabstand lässt sich auch für metrisch skalierte Werte berechnen, während die Berechnung von Standardabweichung, Varianz und Spannweite für ordinalskalierte Werte nicht möglich ist.
Spannweite
Bei der Spannweite handelt es sich um die Differenz zwischen dem kleinsten und dem größten Wert im Datensatz. Da die Bildung von sinnvollen Differenzen voraussetzt, dass diese quantifizierbar sind, d.h. dass mit den Abständen zwischen den Werten gerechnet werden kann, kann die Spannweite nur für metrische Daten berechnet werden – auch wenn es vielleicht kontraintuitiv erscheint, dass etwa eine Spannweite von 5 Notenpunkten bei einer Klassenarbeit keine sinnvolle Größe ist. In Statistik-Klausuren ist das übrigens eine “beliebte” Falle, in die immer wieder Studierende tappen, die auch für nichtmetrische Werte eine Spannweite ausrechnen – hier ist also Vorsicht geboten.
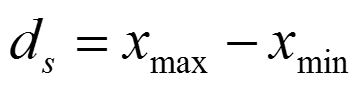
Intuitiv dürfte dagegen die Erkenntnis sein, dass die Spannweite kein robustes Maß für die Streuung ist, da sie von Ausreißern – soweit im Datensatz vorhanden – extrem beeinflusst wird. Tritt an einem Ende der Verteilung mindestens ein Ausreißer auf, findet dieser in jedem Fall Eingang in die Berechnung der Spannweite – gibt es an beiden Enden der Verteilung mindestens einen Ausreißer, wird die Spannweite sogar ausschließlich durch diese bestimmt. Das nachfolgende Beispiel zeigt, wie extrem die Spannweite durch Ausreißer beeinflusst werden kann.
Verteilung A: [100; 120; 170; 280; 290; 300]
Spannweite: ds = 300 – 100 = 200
Verteilung B: [5; 120; 170; 280; 290; 10000]
Spannweite ds = 10000 – 5 = 9995
Aber auch wenn keinerlei Ausreißer im Datensatz vorhanden sind, gibt die Spannweite aufgrund der Tatsache, dass lediglich zwei Werte in ihre Berechnung einfließen, nur ein eher unvollständiges Bild der Streuung wieder, wie anhand eines zweiten Beispiels demonstriert werden soll.
Verteilung A: [100; 100; 110; 115; 118; 300]
Spannweite: ds = 300 – 100 = 200
Verteilung B: [100; 140; 185; 240; 285; 300]
Spannweite: ds = 300 – 100 = 200
Liegen metrisch skalierte Werte vor, ist die Berechnung von Varianz und Standardabweichung also in jedem Fall zu bevorzugen. In der Praxis werden der größte und der kleinste Wert allerdings auch noch für die sogenannte Fünf-Werte-Zusammenfassung benötigt, die weiter unten kurz vorgestellt wird.
Interquartilsabstand (IQR)
Der Interquartilsabstand (nachfolgend als IQR – Inter Quartile Range – abgekürzt) ist als die Differenz zwischen dem oberen und dem unteren Quartil definiert, die wir bereits im Rahmen der statistischen Lagemaße betrachtet haben.
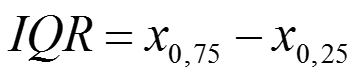
Damit der IQR bestimmt werden kann, muss also die Berechnung der Quartile möglich sein, was wiederum – wie oben bereits angesprochen – mindestens ordinalskalierte Werte voraussetzt. Der IQR kann aber auch für metrisch skalierte Werte kalkuliert werden (Abwärtskompatibilität).
Im Gegensatz zur Spannweite sowie auch zur Varianz und Standardabweichung, die wir im Rahmen des nächsten Statistik-Blogposts besprechen werden, wird der IQR durch Ausreißer nicht beeinflusst und ist somit der einzige im Rahmen dieser Blogserie vorgestellte robuste Dispersionsparameter. Dies lässt sich anhand des weiter oben schon genutzten Beispiels zur Robustheit der Spannweite demonstrieren:
Verteilung A: [100; 120; 170; 280; 290; 300]
IQR = 290 – 120 = 170
Verteilung B: [5; 120; 170; 280; 290; 10000]
IQR = 290 – 120 = 170
Der IQR spielt eine zentrale Rolle bei der Konstruktion von Box-Plots, da er die Höhe der Box bestimmt. Wie ein solcher Box-Plot zu konstruieren ist, wird Thema eines der nächsten Artikel in dieser Blogserie sein.
Fünf-Werte-Zusammenfassung
Bei der sogenannten Fünf-Werte-Zusammenfassung handelt es sich um eine hochkomprimierte Darstellung der Lage sowie der Streuung einer Verteilung, bestehend aus den drei Quartilen (oberes und unteres Quartil sowie Median) sowie dem größten und dem kleinsten Wert.
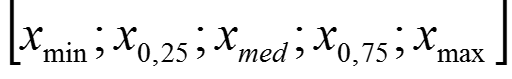
Beispielrechnungen
Im Rahmen einer Befragung machten 30 Probanden Angaben zu ihrem Körpergewicht.
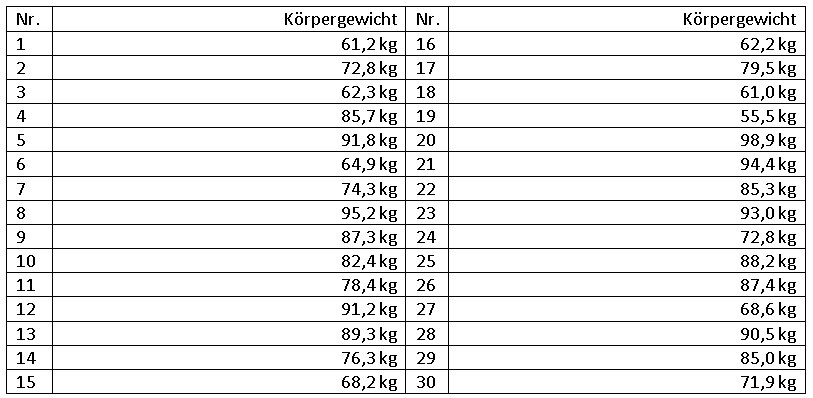
Berechnung der Spannweite
Die Spannweite berechnet sich als Differenz zwischen dem größten und dem kleinsten Wert.
ds = xmax – xmin = 98,9 – 55,5 = 43,4
Die Spannweite beträgt 43,4 kg.
Berechnung des Interquartilsabstands
Für die IQR-Berechnung müssen die Werte zunächst in eine geordnete Reihe gebracht werden.
Werte 1-10: 55,5; 61,0; 61,2; 62,2; 62,3; 64,9; 68,2; 68,6; 71,9; 72,8
Werte 11-20: 72,8; 74,3; 76,3; 78,4; 79,5; 82,4; 85,0; 85,3; 85,7; 87,3
Werte 21-30: 87,4; 88,2; 89,3; 90,5; 91,2; 91,8; 93,0; 94,4; 95,2; 98,9
Für die Berechnung beliebiger Perzentile (die Quartile sind bekanntlich drei Perzentilwerte) greifen wir auf die beiden in der Übungseinheit zu den statistischen Lagemaßen vorgestellten Formeln zurück. Ergibt die Multiplikation der gewünschten Perzentilgrenze p mit der Anzahl der Werte der Verteilung n (d.h. n * p) keinen ganzzahligen Wert, berechnet sich das gesuchte Perzentil wie folgt:
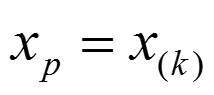
Dabei ist k die jeweils nächste auf das Ergebnis der Multiplikation (n * p) folgende ganze Zahl. Ergibt (n * p) dagegen einen ganzzahligen Wert (in diesem Falle k), berechnet sich das gesuchte Perzentil wie folgt:
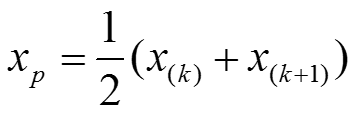
In diesem Fall werden das obere (p = 0,75) und das untere (p = 0,25) Quartil benötigt, d.h.:
(30 * 0,25) = 7,5 -> kein ganzzahliger Wert -> k = 8
-> Der 8. Wert im Datensatz lautet 68,6
(30 * 0,75) = 22,5 -> kein ganzzahliger Wert -> k = 23
-> Der 23. Wert im Datensatz lautet 89,3
IQR = 89,3 – 68,6 = 20,7
Der Interquartilsabstand beträgt 20,7 kg.
Angabe der Fünf-Werte-Zusammenfassung
Vier der fünf für die Fünf-Werte-Zusammenfassung benötigten Werte (größter Wert, kleinster Wert, oberes Quartil und unteres Quartil) sind aus den vorangegangenen Rechnungen bereits bekannt – es wird demnach nur noch der Median gesucht. Da eine gerade Anzahl von Werten (n = 30) vorliegt, wird für die Berechnung des Median auf folgende Formel zurückgegriffen:
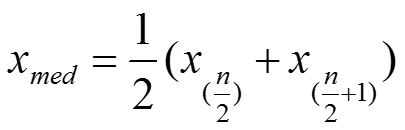
xmed = ½ * (x(30/2) + x(30/2+1))
xmed = ½ * (x15 + x16)
xmed = ½ * (79,5 + 82,4)
xmed = 80,95
Wie bei jeder Perzentilberechnung kann alternativ natürlich auch analog zum oben bereits genutzten Rechenweg vorgegangen werden:
(30 * 0,50) = 15 -> ganzzahliger Wert -> k = 15; k+1 = 16
-> ½ * (79,5 + 82,4) = 80,95
Die Fünf-Werte-Zusammenfassung lautet somit:
[55,50 kg; 68,60 kg; 80,95 kg; 89,30 kg; 98,90 kg]
Übungsaufgaben
Die gleichen 30 Probanden machten außerdem Angaben zu ihrem Alter.
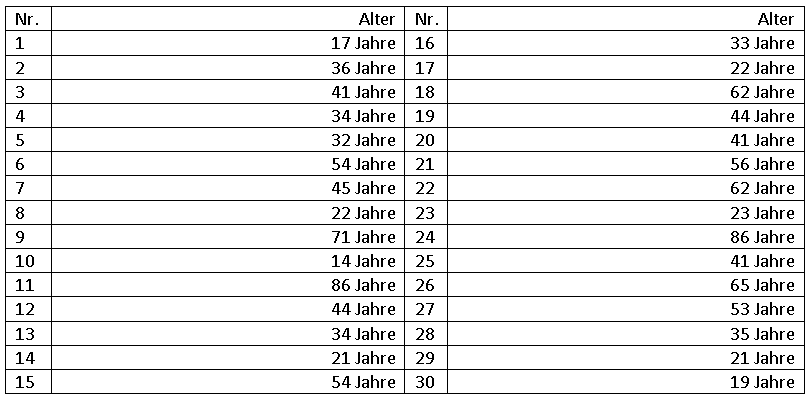
a) Bestimmen Sie die Spannweite.
b) Bestimmen Sie den Interquartilsabstand.
c) Bestimmen Sie die Fünf-Werte-Zusammenfassung.
Zur Anzeige der Lösungen bitte hier klicken.
Die hier vorgestellten Inhalte und Aufgaben sind Teil der Vorlesung “Grundlagen der Statistik” im berufsbegleitenden Bachelor-Studiengang Betriebswirtschaftslehre an der Hochschule Harz. Eine vollständige Übersicht aller Inhalte dieser Vorlesung im Wissenschafts-Thurm findet sich hier: Grundlagen der Statistik.

