In der dieswöchigen Folge des Statistik-Grundlagenkurses hier im “Wissenschafts-Thurm” befassen wir uns mit der Varianz als dem wichtigsten und meistverwendeten Dispersionsparameter. Die Varianz berechnet sich als die Summe der quadrierten Abweichungen aller Einzelwerte einer Verteilung vom arithmetischen Mittel eben dieser Verteilung geteilt durch die Gesamtzahl der Werte.
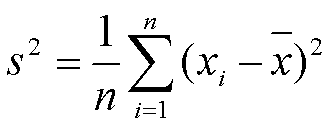
An dieser Stelle lohnt es sich, die Formel nicht nur stur anzuwenden, sondern sie näher zu betrachten – was wird hier eigentlich gerechnet? Zunächst einmal wird die Differenz der einzelnen Werte der Verteilung (x1, x2, x3 … xn) vom arithmetischen Mittel gebildet, die Summe aller Differenzen wird anschließend durch die Anzahl der Werte der Verteilung geteilt. Man errechnet somit quasi das arithmetische Mittel der Differenzen aller Werte vom arithmetischen Mittel – oder anders formuliert die durchschnittliche Abweichung der Werte vom Zentrum der Verteilung. Diese durchaus naheliegende und fast schon intuitive Vorgehensweise für die Bestimmung der Streuung überrascht nur in einem Detail: Die zu addierenden Differenzen werden vorab quadriert um zu verhindern, dass sich positive und negative Abweichungen vom arithmetischen Mittel gegenseitig neutralisieren.
In vielen Formelsammlungen findet sich neben der bekannten Formel auch noch diese, leicht vereinfachte Berechnungsvorschrift:
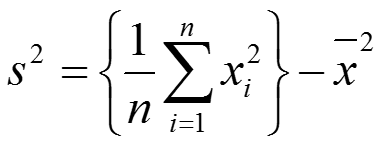
Aufgrund des unumgänglichen Quadrierens ist allerdings auch das Ergebnis eine quadrierte Zahl, d.h. die Varianz einer Gehaltsverteilung steht nicht in der Einheit Euro, sondern in Euro². Dadurch lässt sie sich schlecht interpretieren – oder aber es besteht sogar die Gefahr einer inhaltlichen Fehlinterpretation, wenn die quadrierte Einheit „sinnvoll“ zu sein scheint (z.B. Quadratmeter). Aus diesem Grund wird bei der Berechnung der Varianz meist auch noch die Standardabweichung als positive Wurzel aus der Varianz und damit als „korrekt dimensionierter“ Dispersionsparameter angegeben.
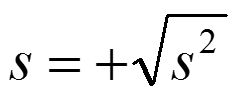
Variationskoeffizient
Wie wir im ersten Blogpost zu den Dispersionsparametern bereits gelernt haben, spielen die Streuungsmaße unter anderem beim Vergleich von Verteilungen eine wichtige Rolle. Hierbei kann es erforderlich werden, die Standardabweichung in eine dimensionslose Größe umzuwandeln, um einen Vergleich der Streuung von Verteilungen zu ermöglichen, die in verschiedenen Dimensionen erfasst werden. Als Beispiel sei auf den Vergleich von Preisverteilungen in Euro und mexikanischen Pesos verwiesen.
Da ein Euro etwa 20 Pesos entspricht, besteht bei einem direkten Vergleich der Standardabweichungen beider Verteilungen das Risiko, die Streuung der Preisangaben in Pesos im Verhältnis zu den Preisangaben in Euro aufgrund der größeren absoluten Differenzwerte erheblich zu überschätzen. Aus diesem Grund dividiert man die Standardabweichungen beider Verteilungen vor dem Vergleich noch durch die jeweiligen arithmetischen Mittel und generiert somit den dimensionslosen Variationskoeffizienten, mit dem ein Vergleich möglich wird. Die Berechnung des Variationskoeffizienten ist jedoch nur gestattet, wenn das arithmetische Mittel der Verteilung positiv ist.
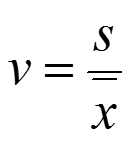
Empirische Varianz und Stichprobenvarianz
Im Rahmen dieser Blog-Serie arbeiten wir mit der sogenannten empirischen Varianz:
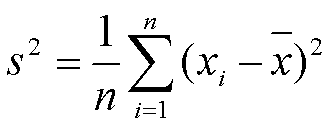
Bei der Berechnung von Varianzen mit SPSS, PSPP und anderen statistischen Analyseprogrammen wird dagegen meist die sogenannte Stichprobenvarianz berechnet; dann aber nicht als solche, sondern als “Varianz” deklariert, was zu erheblicher Verwirrung bei Studierenden führen kann, die ihre Übungslösungen mit Hilfe von Software überprüfen möchten. Die Stichprobenvarianz unterscheidet sich von der empirischen Varianz darin, dass anstatt durch die Anzahl der Werte der Verteilung durch die Anzahl an Freiheitsgraden (n – 1) dividiert wird – ein Begriff, auf den in einem späteren Blogpost noch einmal näher eingegangen werden wird.
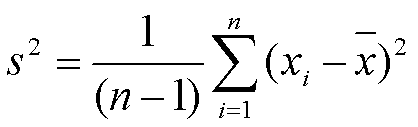
Beispielrechnungen
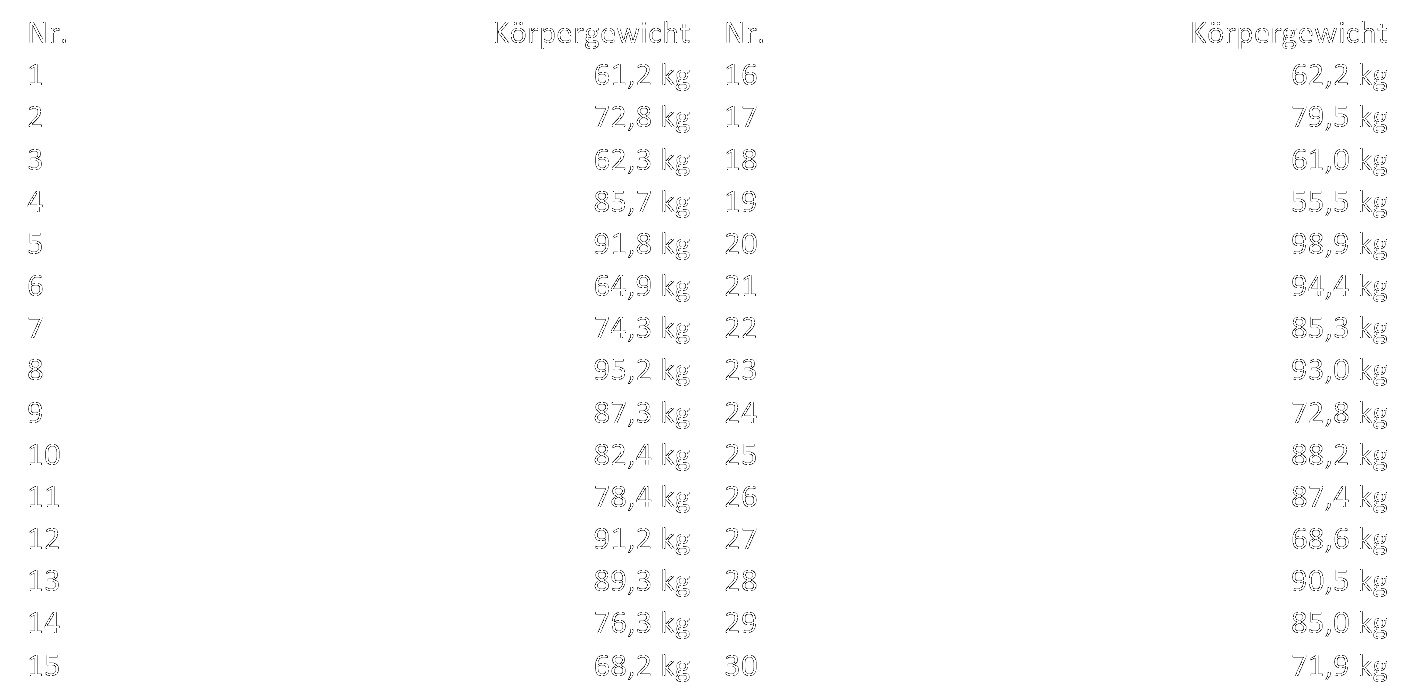
Für die Beispielrechnung greifen wir auf die Daten aus einem der letzten Blogposts zurück – Angaben zum Körpergewicht von 30 Probandinnen und Probanden.
Berechnung der Varianz
Für die Berechnung der Varianz empfiehlt sich die Anlage einer Hilfstabelle, über die sich die beiden benötigten Größen – das arithmetische Mittel sowie die Summe der quadrierten Abstände der Werte vom arithmetischen Mittel – schnell und einfach ermitteln lassen.
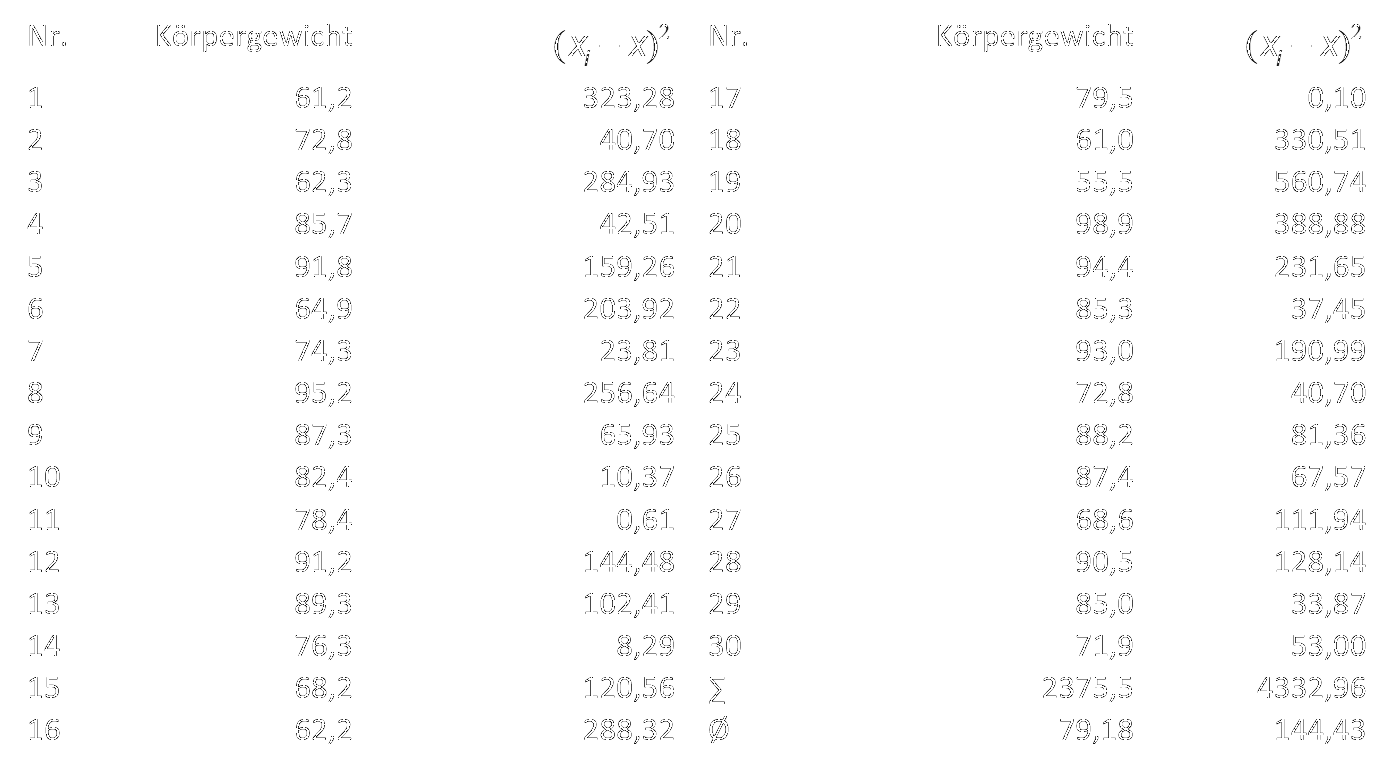
Die Varianz dieser Verteilung liegt bei 144,43 kg².
(Für alle Softwarenutzer: Die Stichprobenvarianz liegt bei 149,41 kg².)
Berechnung der Standardabweichung
Die Standardabweichung berechnet sich als positive Wurzel aus der Varianz und liegt bei 12,02 kg. (Für alle Softwarenutzer: Die Wurzel der Stichprobenvarianz beträgt 12,22 kg.)
Da hier keine unterschiedlich dimensionierten Verteilungen miteinander verglichen werden sollen (zum Beispiel eine Gewichtsverteilung in kg und eine Gewichtsverteilung in g) erübrigt sich an dieser Stelle die Bestimmung des Variationskoeffizienten.
Übungsaufgaben
Auch bei dieser Übungsaufgabe bleiben wir bei den Beispieldaten aus der vergangenen Übungseinheit – den Altersangaben der 30 schon nach ihrem Körpergewicht befragten Probandinnen und Probanden.
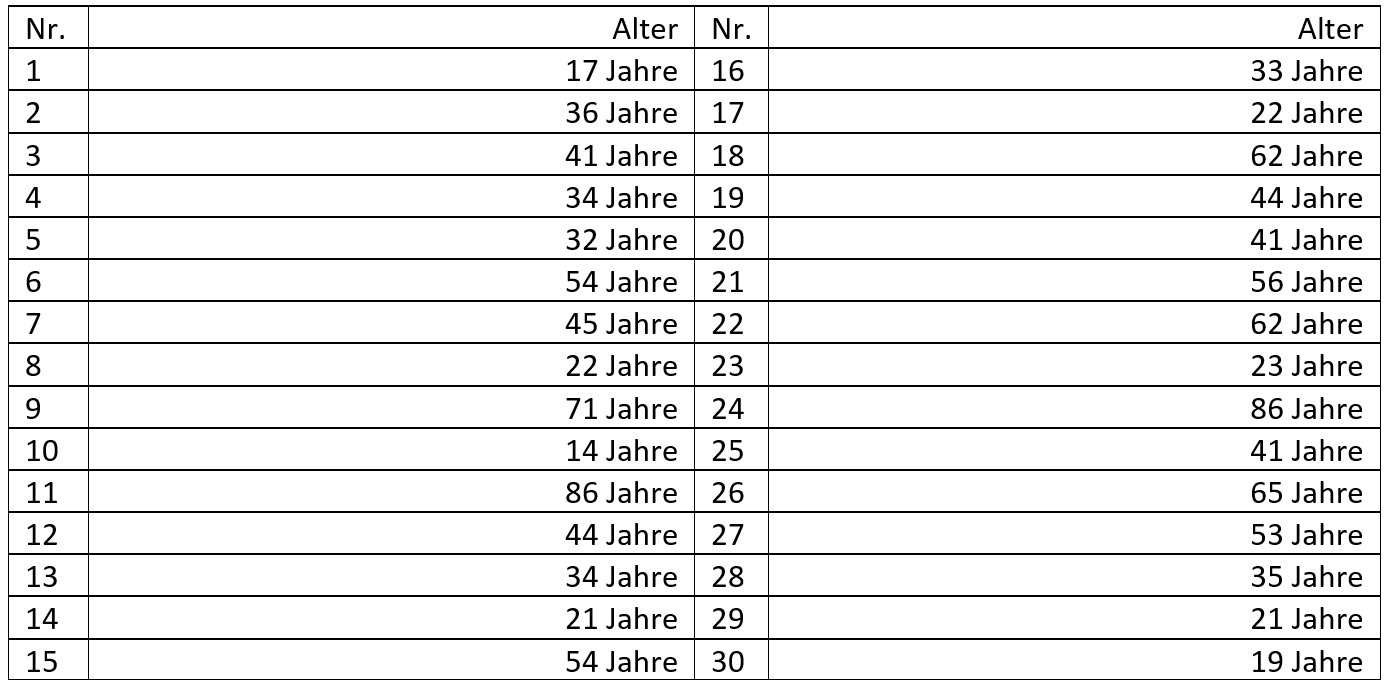
a) Bestimmen Sie die Varianz.
b) Bestimmen Sie die Standardabweichung.
Zur Anzeige der Lösungen bitte hier klicken.
Die hier vorgestellten Inhalte und Aufgaben sind Teil der Vorlesung “Grundlagen der Statistik” im berufsbegleitenden Bachelor-Studiengang Betriebswirtschaftslehre an der Hochschule Harz. Eine vollständige Übersicht aller Inhalte dieser Vorlesung im Wissenschafts-Thurm findet sich hier: Grundlagen der Statistik.

