Der Box-Plot (oder auch Box-and-Whisker-Plot) ist eine der wohl spannendsten grafischen Darstellungsformen, welche die deskriptive Statistik zu bieten hat. In dieser einen Grafik finden sich komprimiert Angaben zu einer Vielzahl von Verteilungsparametern wieder, die wir in den vorangegangenen Blogposts betrachtet haben. So kann man neben Lagemaßen (Median, Quartilswerte) auch Streuungsmaße (Spannweite, Interquartilsabstand) sowie die Form der Verteilung (d.h. linkssteil, symmetrisch oder rechtssteil) direkt aus dem Box-Plot ablesen – und sogar über das Vorhandensein von Ausreißern im Datensatz lässt sich auf Basis der Konstruktionsvorschrift für den Box-Plot eine Feststellung treffen. Der Box-Plot gestattet also Aussagen über Zentrum, Streuung, Form und Ausreißer einer Verteilung und bietet somit eine besonders hohe Informationsdichte. Ein noch größeres Informationspotential entfaltet der Box-Plot beim Vergleich von Verteilungen durch das Nebeneinanderstellen mehrerer Grafiken.
Bei der Konstruktion von Box-Plots wird in einfache Box-Plots (bei denen die Zäune jeweils bis zum größten sowie bis zum kleinsten Wert im Datensatz reichen) und in sogenannte erweiterte Box-Plots (bei deren Konstruktion die Grenzen der Zäune über den Interquartilsabstand berechnet und in denen Ausreißer und Extremwerte ausgewiesen werden) unterschieden. Nachfolgend wird in diesem Blogpost nur der erweiterte Box-Plot betrachtet. Ein solcher erweiterter Box-Plot besteht aus drei Komponenten: Der eigentlichen Box, den Zäunen der Box sowie möglicherweise einzuzeichnenden Ausreißern oder Extremwerten, sollten solche im Datensatz auftauchen. Die Konstruktion eines erweiterten Box-Plots erfolgt demnach ebenfalls in drei Schritten.
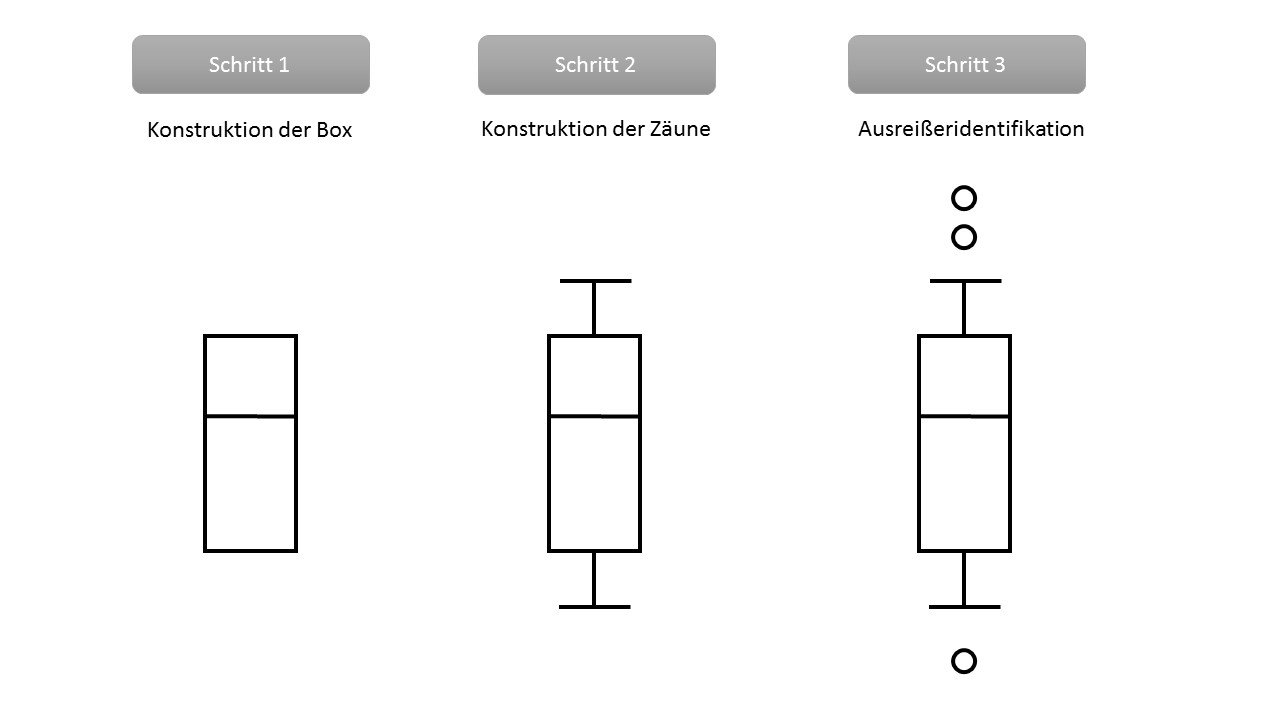
Schritt 1: Konstruktion der Box. Hierfür werden drei Werte benötigt: Das obere Quartil (obere Grenze der Box), das untere Quartil (untere Grenze der Box) sowie der Median (dieser wird als zusätzliche Linie in die Box eingezeichnet). Sollte der Median mit einem der beiden Quartilswerte identisch sein, wird die entsprechende Grenze einfach mit doppelter Strichstärke gekennzeichnet. Sind alle drei Quartilswerte identisch, kann keine Box konstruiert werden – in diesem Fall wird die Box durch eine dicke Linie an der Stelle x0,75 = x0,50 = x0,25 ersetzt (die Zäune und Ausreißer könnten aber auch bei einer solchen Verteilung existieren).
Aus der Lage des Medians innerhalb der Box lässt sich übrigens eine Aussage über die Form der Verteilung herauslesen: Liegt der Median (ungefähr) in der Mitte, handelt es sich um eine symmetrische Verteilung, liegt der Median dagegen nahe der unteren Grenze der Box, so ist die Verteilung rechtsschief und linkssteil. Liegt der Median nahe an der oberen Grenze der Box, so ist die Verteilung dementsprechend rechtssteil und linksschief. Der Box-Plot kann daher (zum Beispiel in einer Klausur) als visuelle Kontrolle für die Richtigkeit der Berechnung des Momentenkoeffizienten oder des Quartilskoeffizienten der Schiefe herangezogen werden.
Schritt 2: Konstruktion der Zäune. Da die Box vom oberen zum unteren Quartil verläuft, entspricht ihre Höhe genau dem Interquartilsabstand. Die Berechnung des IQR liefert uns die benötigten Angaben für das Einzeichnen der Zäune. Der 1,5-fache Wert des IQR wird nämlich zum oberen Quartilswert addiert bzw. vom unteren Quartilswert subtrahiert, um die virtuellen (aber nicht einzuzeichnenden – ein typischer Fehler in Klausuren) Maximal- bzw. Minimalwerte für die Grenzen der Zäune zu ermitteln. Anschließend wird der größte Wert bzw. der kleinste Werte im Datensatz ermittelt, der noch in den Bereich x0,75 + 1,5 IQR bzw. in den Bereich x0,25 – 1,5 IQR fällt. Der obere bzw. der untere Zaun werden dann bis zu diesen Werten gezeichnet – aber auch nur bis zu diesen und nicht bis zu den errechneten maximalen Grenzwerten.
In der Praxis kann es vorkommen, dass der obere Zaun, der untere Zaun oder auch beide Zäune entfallen, da keine Werte aus dem Datensatz in den benannten Bereichen liegen. Auch kann der Fall eintreten, dass Zäune genau bis zu den Maximal- bzw. Minimalwerten reichen, weil sich reale Werte im Datensatz exakt an der Stelle x0,75 + 1,5 IQR bzw. an der Stelle x0,25 – 1,5 IQR befinden. Von beiden Fällen sollte man sich also keinesfalls irritieren lassen – insbesondere nicht in einer Klausur.
Schritt 3: Identifikation von Ausreißern und Extremwerten. Liegen Werte im Datensatz oberhalb von x0,75 + 1,5 IQR bzw. unterhalb von x0,25 – 1,5 IQR, handelt es sich um Ausreißer. Beim erweiterten Box-Plot wird dabei noch in Ausreißer und „extreme“ Ausreißer – die sogenannten Extremwerte – unterschieden, indem eine weitere „virtuelle“ Grenze basierend auf dem IQR errichtet wird. Werte, die zwischen x0,75 + 1,5 IQR und x0,75 + 3 IQR bzw. zwischen x0,25 – 1,5 IQR und x0,25 – 3 IQR liegen, werden als „normale“ Ausreißer mit einem Kreis markiert. Werte, die sogar noch außerhalb dieser Bereiche liegen, gelten als Extremwerte und sind mit einem Sternchen zu markieren. Sowohl die Ausreißer als auch die Extremwerte werden in der Regel noch mit der fortlaufenden Nummer des Datensatzes versehen, um diesen in nachfolgenden Untersuchungen schneller auffinden zu können.

Wie schon bei der Konstruktion der Zäune, kann es auch bei der Identifikation von Ausreißern und Extremwerten vorkommen, dass in einer oder auch in beiden Richtungen keine entsprechenden Werte zu finden sind und daher nichts in den Box-Plot eingezeichnet wird. Auch hiervon sollte man sich – sollte ein solcher Fall mal in einer Klausur vorkommen – also nicht irritieren lassen.
Da in der deskriptiven Statistik keine allgemeingültige Definition für Ausreißer existiert, kann es im übrigen auch an anderer Stelle (etwa bei Unklarheiten über die Einordnung eines Wertes als Ausreißer) sinnvoll sein, auf das Konstruktionsprinzip des Box-Plots zurückzugreifen. Die Unterscheidung in Ausreißer und extreme Ausreißer ist außerhalb der Box-Plot-Konstruktion allerdings eher unüblich.
Beispielgrafik
Auf dem Campus der Hochschule Harz haben wir 20 willkürlich ausgewählte Studierende nach ihrem Alter (in ganzen Jahren) befragt. Dabei ergab sich die folgende Verteilung:
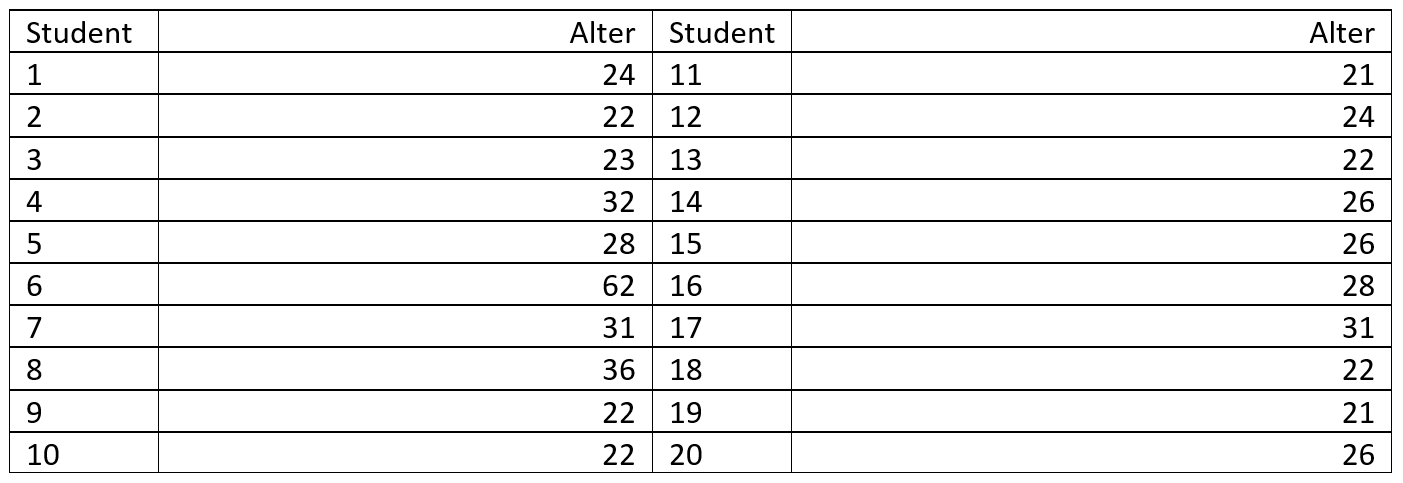
Da für die Konstruktion des Box-Plots die Quartilswerte und der Interquartilsabstand berechnet werden müssen, lohnt sich im ersten Schritt das Festhalten der geordneten Verteilung:
21; 21; 22; 22; 22; 22; 22; 23; 24; 24; 26; 26; 26; 28; 28; 31; 31; 32; 36; 62
Da (n * p) jeweils einen ganzzahligen Wert (k) ergibt, berechnen sich die Quartile wie folgt:
(n*p) = (20 * 0,25) = 5 -> k = 5; k+1 = 6 -> xp = (22+22)/2 = 22
(n*p) = (20 * 0,50) = 10 -> k = 10; k+1 = 11 -> xp = (24+26)/2 = 25
(n*p) = (20 * 0,75) = 15 -> k = 15; k+1 = 16 -> xp = (28+31)/2 = 29,5
Der IQR lässt sich nun ohne großen Aufwand bestimmen:
IQR = 29,5 – 22 = 7,5
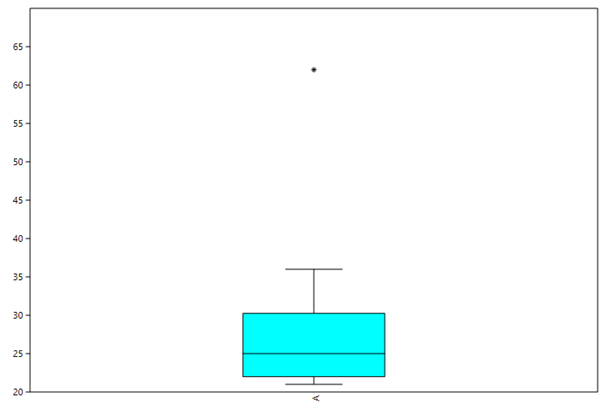
Die Box wird im ersten Schritt also von 29,5 (obere Grenze) zu 22 (untere Grenze) gezeichnet, der Median wird bis 25 eingetragen. Da der 1,5-fache IQR bei 11,25 liegt, endet der obere Zaun beim größten Wert zwischen 29,5 und 40,75 (36), der untere Zaun beim kleinsten Wert zwischen 22 und 10,75 (21). Da die 21 bereits den kleinsten Wert der Verteilung darstellt, können im unteren Bereich des Box-Plots weder Ausreißer noch Extremwerte liegen. Ausreißer im oberen Bereich der Verteilung müssten zwischen 40,75 und 52 liegen – hier finden sich in der Tabelle allerdings ebenfalls keine Werte. Der noch verbliebene Wert von 62 stellt damit einen Extremwert dar.
Der mit Hilfe der Software PAST berechnete erweiterte Box-Plot sieht am Ende also wie folgt aus:
Übungsaufgabe
Parallel zur Befragung der 20 Studierenden wurden auch 20 willkürlich ausgewählte Professorinnen und Professoren der Hochschule Harz nach ihrem Alter befragt. Dabei ergab sich folgendes Bild:

1) Konstruieren Sie einen erweiterten Box-Plot.
Zur Anzeige der Lösungen bitte hier klicken.
Die hier vorgestellten Inhalte und Aufgaben sind Teil der Vorlesung “Grundlagen der Statistik” im berufsbegleitenden Bachelor-Studiengang Betriebswirtschaftslehre an der Hochschule Harz. Eine vollständige Übersicht aller Inhalte dieser Vorlesung im Wissenschafts-Thurm findet sich hier: Grundlagen der Statistik.


Warum gelten diese Regeln zur Berechnung des Boxplots nur wenn alle Werte positiv sind? Sobald man negative Werte im Datensatz hat, weichen händisch berechneten Boxplots von der Softwarelösung ab.
@Dan: In der Tat zielt die hier vorgestellte Konstruktionsvorschrift für Box-Plots – wie man sie auch in den meisten Lehrbüchern und Tutorials findet – auf Datensätze ohne negative Werte ab. Wie man die Probleme, die sich bei negativen Werten im Datensatz mit der grafischen Darstellung ergeben, umgehen und trotzdem einen schönen Box-Plot generieren kann, wird z.B. in diesem lesenswerten Blogpost (weiter unten) beschrieben:
http://www.real-statistics.com/excel-capabilities/special-charting-capabilities/