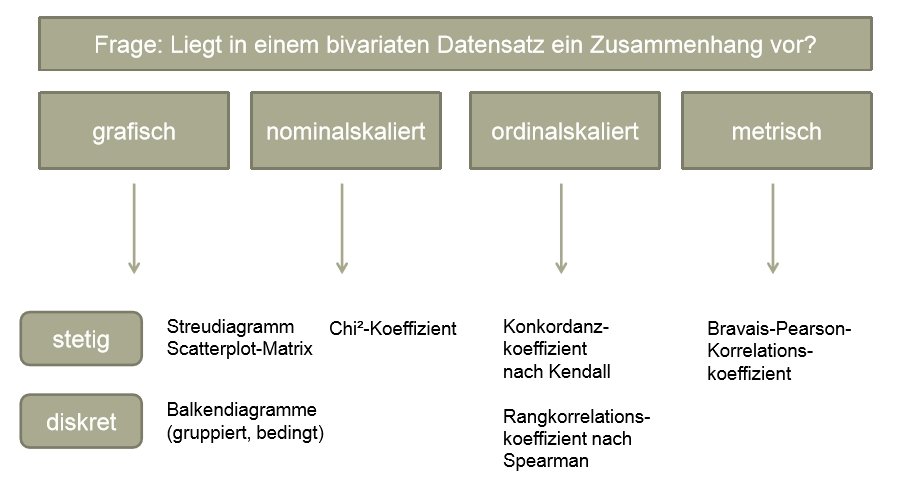
Was sind Zusammenhangsmaße?
Während wir bislang immer nur eine Variable x (Lagemaße, Streuungsmaße, Schiefe und Wölbung, Grafiken) einzeln analysiert haben, sollen in den nachfolgenden Blogbeiträgen zwei Variablen x und y gleichzeitig betrachtet werden, um festzustellen, ob zwischen diesen ein Zusammenhang besteht. Dabei gilt, dass ein solcher Zusammenhang unterstellt werden kann – aber nicht existieren muss – wenn die Variablen miteinander korrelieren (d.h. sich gleichmäßig zueinander verhalten). Hierbei wird in gleichsinnige Korrelationen (größere x-Werte fallen mit größeren y-Werten, kleinere x-Werte fallen mit kleineren y-Werten zusammen) und gegensinnige Korrelationen (größere x-Werte fallen mit kleineren y-Werten, kleinere x-Werte fallen mit größeren y-Werten zusammen) unterschieden. Die Stärke solcher Korrelationen (nicht aber die Stärke eines möglichen inhaltlichen Zusammenhangs) wird über sogenannte Zusammenhangsmaße wiedergegeben, von denen wir in den nachfolgenden Blogposts vier (Bravais-Pearson, Spearman, Kendall, Chi²) kennenlernen werden.
Welches Zusammenhangsmaß sich berechnen lässt, hängt – wie so vieles in der Statistik – vom Skalenniveau der betrachteten Variablen ab. Liegen nominalskalierte Variablen vor, eignet sich der Chi2-Koeffizient, für ordinalskalierte Variablen empfehlen sich der Rangkorrelationskoeffizient nach Spearman oder auch der Konkordanzkoeffizient nach Kendall, während sich für metrisch skalierte Daten der Bravais-Pearson-Korrelationskoeffizient anbietet (wenn eine lineare Korrelation vermutet wird – dazu später mehr).
Wie so oft in der Statistik ist die Berechnung „abwärtskompatibel“, nicht aber „aufwärtskompatibel“, d.h. für metrisch skalierte Daten können auch der Chi2-Koeffizient oder der Konkordanzkoeffizient nach Kendall berechnet werden, für ordinalskalierte Daten aber niemals der Bravais-Pearson-Korrelationskoeffizient. Immer möglich ist auch die (unterstützende) grafische Zusammenhangsanalyse von Daten, wobei sich für diskrete Daten die Konstruktion gruppierter oder bedingter Balkendiagramme, für stetige Daten dagegen die Konstruktion von zwei- und dreidimensionalen Streudiagrammen und Scatterplot-Matrizen empfiehlt.
Korrelation und Kausalität
Von wesentlicher Bedeutung für die Interpretation von Zusammenhangsmaßen ist die Verinnerlichung der Tatsache, dass identifizierte Korrelationen zwar näher untersucht, niemals jedoch unmittelbar inhaltlich interpretiert werden sollten – auch dann nicht, wenn sich eine Interpretation im Hinblick auf einen sachlogischen Zusammenhang zwischen den betrachteten Variablen geradezu aufdrängt. Untersucht man beispielsweise den Zusammenhang zwischen Preis und Verkaufszahlen und identifiziert dabei eine starke Korrelation zwischen beiden Variablen, ist es zwar durchaus logisch davon auszugehen, dass der Preis die Verkaufszahlen beeinflusst (und nicht umgekehrt) – auf Basis eines Zusammenhangsmaßes lässt sich diese Annahme jedoch keinesfalls beweisen, da alle im Rahmen dieser Blogserie betrachteten Zusammenhangsmaße keine Wirkungsrichtung (x beeinflusst y, y ist abhängig von x) kennen. Tatsächlich kann jede entdeckte Korrelation zweier Variablen auf vier mögliche Ursachen zurückzuführen sein, die wir nachfolgend kurz betrachten wollen.
Möglichkeit 1: Es liegt ein „echter“ inhaltlicher Zusammenhang mit einseitiger Wirkungsrichtung vor, d.h. x beeinflusst tatsächlich y bzw. y ist tatsächlich abhängig von x. Fälschlicherweise wird leider oft davon ausgegangen, dass eine starke Korrelation immer auf einen solchen monokausalen Zusammenhang zurückzuführen ist bzw. diesen sogar irgendwie „beweist“. Diesen Fehler sollte man (ganz besonders in einer Klausur) nach Möglichkeit vermeiden.
Möglichkeit 2: Es handelt sich um einen sogenannten beidseitigen Zusammenhang, d.h. x beeinflusst y während y gleichzeitig auch x beeinflusst. Dies ist etwa beim Bekanntheitsgrad eines Produktes und dessen Verkaufszahlen der Fall, da die Bekanntheit einerseits die Verkaufszahlen beeinflusst (ein stark beworbenes Produkt ist bekannter und wird häufiger angefragt), gleichzeitig aber auch die Verkaufszahlen den Bekanntheitsgrad beeinflussen (ein Produkt, das sich etwa über eine Niedrigpreisstrategie viel verkauft, wird mit der Zeit immer bekannter). Derartige beidseitige Zusammenhänge lassen sich nur mit statistischen Komplexverfahren näher untersuchen, die wir im Rahmen unserer Statistik-Blogserie nicht betrachten werden. Die besondere Schwierigkeit bei der Analyse solcher beidseitigen Zusammenhänge besteht – wie man sich vermutlich leicht vorstellen kann – darin festzustellen, welcher Anteil des Zusammenhangs sich auf welche Wirkungsrichtung (x -> y; y -> x) zurückführen lässt.
Möglichkeit 3: Es handelt sich um einen rein zufälligen Effekt – eine sogenannte Scheinkorrelation. Prüft man nämlich nur genügend Variablen gegeneinander, wird man immer Kombinationen finden, bei denen sich allein durch Zufall eine starke Korrelation ergibt. In meiner Vorlesung verweise ich diesbezüglich gerne auf die Internetseite des US-Juristen Tyler Vigen, der seit Jahren Korrelationen (ausgedrückt über den Bravais-Pearson-Korrelationskoeffizienten) sammelt, bei denen ein inhaltlicher Zusammenhang extrem unplausibel sein dürfte. Auf http://www.tylervigen.com/spurious-correlations finden sich viele ganz hervorragende Beispiele dafür, warum eine – auch sehr starke – Korrelation noch lange nicht belegt, dass zwischen den betrachteten Variablen auch ein kausaler Zusammenhang existiert – so zum Beispiel zwischen der Scheidungsrate im US-Bundesstaat Maine und dem Pro-Kopf-Konsum von Margarine (r = 0,99258) oder dem Pro-Kopf-Konsum von Mozzarella und der Anzahl an Doktoranden/innen im Bereich der Ingenieurswissenschaften (r = 0,958648).
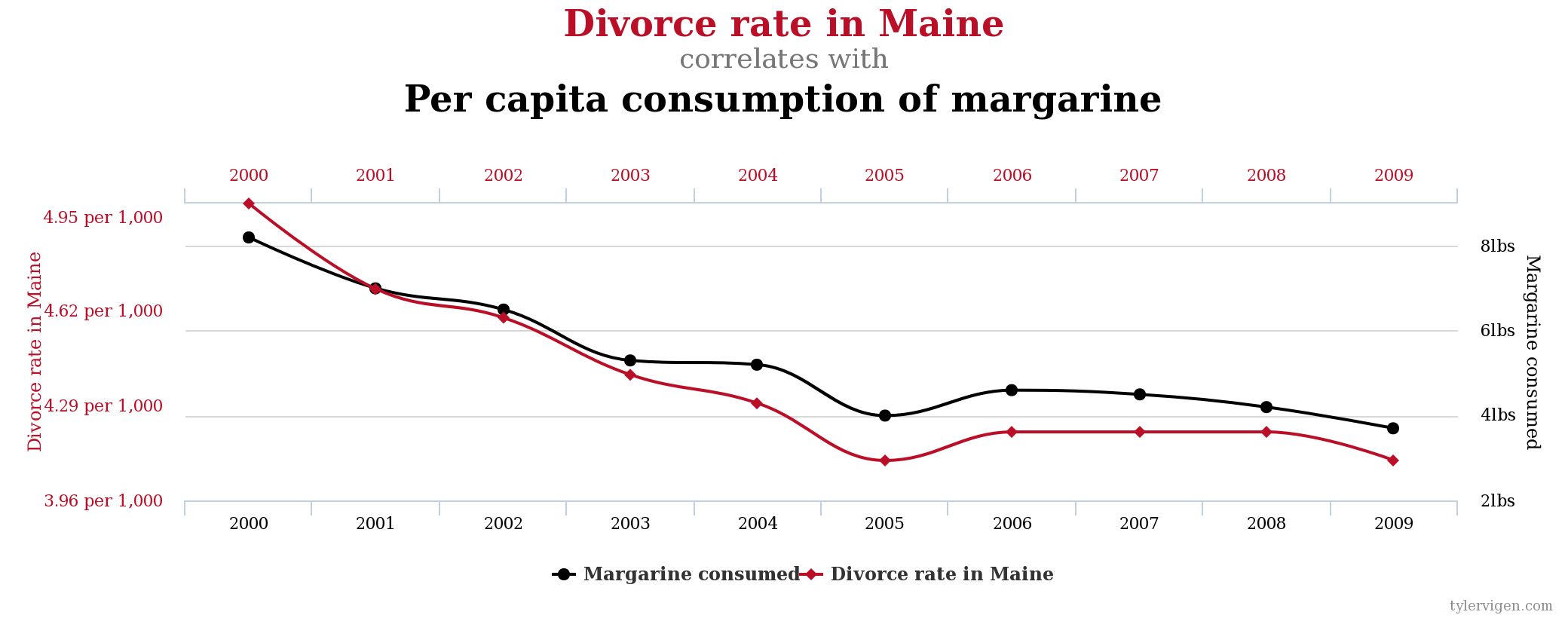
Als Nebenbemerkung sei an dieser Stelle darauf hingewiesen, dass Untersuchungsdesigns, die auf dem wahllosen „Durchspielen“ einer Vielzahl von Korrelationsmöglichkeiten ohne die vorherige Aufstellung inhaltlich begründeter Vermutungen und Forschungsfragen basieren, aufgrund der Existenz derartiger Scheinkorrelationen abzulehnen sind. Testet man nämlich einfach nur genügend Kombinationen von Variablen durch, werden sich letztlich immer starke oder sogar sehr starke Korrelationen finden lassen, die jedoch nicht notwendigerweise auf einen inhaltlichen Zusammenhang zurückzuführen sind. Wir werden dieser wichtigen Problematik in einem späteren Blogpost bei der Betrachtung statistischer Testverfahren unter dem Stichwort „p-value hacking“ erneut begegnen.
Möglichkeit 4: Es handelt sich um einen indirekten Zusammenhang zwischen x und y über eine dritte, nicht betrachtete Variable z. Das geradezu klassische Beispiel hierfür ist die über die Jahre mehrfach bestätigte, äußerst starke Korrelation zwischen der Geburtenrate und der Anzahl von Störchen in deutschen Landkreisen. Obwohl zwischen beiden Variablen – natürlich – kein unmittelbarer Zusammenhang besteht, sind sie doch über eine dritte Variable – den Grad der Urbanisierung – miteinander verbunden. Da der Urbanisierungsgrad sowohl die Geburtenquote (aus soziologischen Gründen) als auch die Storchdichte (aus ökologischen Gründen) gleichermaßen beeinflusst, sind beide Variablen deutlich gleichläufig. Auch die Möglichkeit eines solchen Zusammenhangs sollte bei der Interpretation von Korrelationen nicht voreilig ausgeschlossen werden – bei betriebs- oder volkswirtschaftlichen Fragestellungen finden sich derartige „Hintergrundzusammenhänge“ in der Praxis sogar recht häufig.
Da eine starke Korrelation zweier Variablen theoretisch auf jede dieser vier Möglichkeiten zurückzuführen sein kann, sollte man sich vor der kausalen Interpretation von Korrelationen tunlichst hüten – auch wenn der inhaltliche Zusammenhang sich vermeintlich „offensichtlich“ präsentiert. Eine Korrelation ist stets nur als ein Hinweis darauf zu begreifen, welche möglichen Zusammenhänge sich für eine vertiefte Analyse mit weiterführenden statistischen Verfahren (insbesondere Tests) anbieten. In vielen Vorlesungen und Lehrbüchern wird diese zentrale Erkenntnis über den bekannten Merksatz „Korrelation ist nicht gleich Kausalität“ vermittelt.
Die hier vorgestellten Inhalte und Aufgaben sind Teil der Vorlesung “Grundlagen der Statistik” im berufsbegleitenden Bachelor-Studiengang Betriebswirtschaftslehre an der Hochschule Harz. Eine vollständige Übersicht aller Inhalte dieser Vorlesung im Wissenschafts-Thurm findet sich hier: Grundlagen der Statistik.


Ich habe diese Abhandlung gerne gelesen. Die Beispiele sind anschaulich und warnen hoffentlich allzu “Gläubige” an Algorithmen vor voreiligen Schlüssen.
Jürgen Scharf
@Jürgen Scharf: Vielen Dank! Das Lob eines Mathematikers freut uns hier natürlich ganz besonders. Schöne Grüße nach Magdeburg!
ich würde gerne wissen, von wem diese aussage stammt: Korrelation ist nicht gleich Kausalität oder anders formuliert: wem wird diese aussage zugeordnet oder hat sie als erster ausgeführt/ angeführt.
wäre für mich sehr wichtig, weil ich eine arbeit schreibe wo dies vorkommt und ich würde gerne die quelle zitieren können.
danke
@Manfred Dellemann: Das ist eine äußerst spannende Frage – darüber habe ich noch nie nachgedacht. Vielen Dank dafür! Ich werde das mal recherchieren und schauen, ob ich eine brauchbare Antwort für Sie finden kann.
Sehr gut und verständlich dargelegte 4 Ursachen einer starken Korrelation. Wir haben genau das letzte Woche in der Vorbereitungswoche der Seminarfacharbeit für SEKII diskutiert. Viele Schülerteams erwägen u.a. eine Umfrage zu machen.
Frage: Wie ist die Aussage zu einer NICHT vorhandenen, bzw. sehr schwachen Korrelation? Ist ein Faktor von r=0… 0,1 ein starkes Indiz dafür, dass die beiden Variablen NICHT in einen kausalen Zusammenhang stehen? Natürlich könnte eine dritte Variable einen tatsächlich existierenden Zusammenhang “auslöschen”.
Nette Grüße aus Thüringen
von einem Mathe-Pauker 😉
@Jörg Kleinstüber: Vielen Dank für die freundliche Rezension und natürlich die interessante Frage. Sicher ist, dass das Vorhandensein einer Korrelation nicht zwangsweise bedeuten muss, dass auch ein inhaltlicher Zusammenhang existiert – aber könnte es umgekehrt ein Szenario geben, in dem ein Korrelationskoeffizient sehr niedrig ausfällt, obwohl eigentlich doch ein Zusammenhang besteht?
Ich würde das bejahen. Insbesondere zwei Möglichkeiten fallen mir ad hoc ein:
a) Man testet mit dem für den Zusammenhang falschen Korrelationskoeffizienten. Bei einem perfekten monotonen Zusammenhang, der aber nicht linear ist, wird der Bravais-Pearson niedrig ausfallen – ebenso wie man einen niedrigen Wert für Spearman oder Kendall erwarten müsste, würde man sie auf einen bivariaten Datensatz anwenden, der eine exakte Cosinusfunktion beschreibt. In beiden Fällen läge ein sehr starker Zusammenhang vor – nur eben nicht von der Art, die man mit dem jeweiligen Korrelationskoeffizienten aufspüren kann. Insofern ist z.B. ein niedriger Wert für Bravais-Pearson oder Kendall in der Tat kein Beleg dafür, dass im untersuchten Datensatz keine Korrelation existiert – sondern nur eben dafür, dass (wahrscheinlich, siehe nächster Punkt) keine lineare bzw. monotone Korrelation vorliegt.
2) Schon ein einziger Ausreißer im Datensatz kann das Ergebnis einer Korrelationsanalyse erheblich beeinflussen – man denke etwa an den Leverage-Effekt bei der linearen Regression. Befinden sich also Ausreißer (uni- wie bivariate) im Datensatz, kann die Berechnung eines Korrelationskoeffizienten ohne vorherige Bereinigung des Datensatzes in der Tat dazu führen, dass sich ein schwacher Korrelationswert ergibt, obwohl tatsächlich eine sehr starke Korrelation vorliegt.