AUFGABE
In einer Rinderzucht werden zehn ausgewachsene Tiere verschiedenen Alters gewogen.
| Nr. | Gewicht (in kg) | Alter (in Jahren) |
| 01 | 563 | 15 |
| 02 | 701 | 21 |
| 03 | 523 | 13 |
| 04 | 521 | 12 |
| 05 | 618 | 16 |
| 06 | 633 | 18 |
| 07 | 571 | 16 |
| 08 | 671 | 20 |
| 09 | 710 | 22 |
| 10 | 512 | 10 |
Berechnen Sie den Rangkorrelationskoeffizienten nach Spearman.
Der für die Lösung dieser Aufgabe erforderliche theoretische Hintergrund lässt sich hier noch einmal nachlesen. Die Musterlösung findet sich dann unterhalb des Pfeils.
 MUSTERLÖSUNG
MUSTERLÖSUNG
Kurzfassung der erforderlichen Lösungsschritte:
1) Zuweisung der Ränge für beide Variablen (bitte auf verbundene Ränge achten).
2) Berechnung der Rangplatzdifferenzen und der quadrierten Rangplatzdifferenzen.
3) Einsetzen der Summe der quadrierten Rangplatzdifferenzen in die Spearman-Formel.
| Nr. | Gewicht (in kg) | Rang (Gewicht) | Alter (in Jahren) | Rang (Alter) | Differenz (d) | Differenz² (d²) |
| 01 | 563 | 4 | 15 | 4 | 0 | 0 |
| 02 | 701 | 9 | 21 | 9 | 0 | 0 |
| 03 | 523 | 3 | 13 | 3 | 0 | 0 |
| 04 | 521 | 2 | 12 | 2 | 0 | 0 |
| 05 | 618 | 6 | 16 | 5,5 | 0,5 | 0,25 |
| 06 | 633 | 7 | 18 | 7 | 0 | 0 |
| 07 | 571 | 5 | 16 | 5,5 | -0,5 | 0,25 |
| 08 | 671 | 8 | 20 | 8 | 0 | 0 |
| 09 | 710 | 10 | 22 | 10 | 0 | 0 |
| 10 | 512 | 1 | 10 | 1 | 0 | 0 |
Summe der quadrierten Rangplatzdifferenzen: 0,5
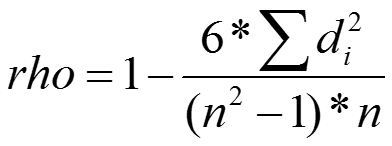
Spearmans rho = 1 – [(6*0,5) / (10²-1)*10] = 1 – 3/990 = 0,9969
Es liegt eine starke (fast perfekte) positive monotone Korrelation vor.
>>> Zurück zur Übersichtsseite Statistik.
Diese Übungsaufgabe stammt aus der Vorlesung “Grundlagen der Statistik” von Christian Reinboth im berufsbegleitenden Bachelor-Studiengang BWL an der Hochschule Harz.
