(Der Blog-Beitrag zu dieser Übung findet sich hier.)
Arithmetisches Mittel
Aus einem Produktionslos von 1.000 Karosserieteilen wird eine Stichprobe von 20 Teilen gezogen und gewogen. Es ergeben sich die folgenden Werte:
a) Fassen Sie diese Werte in einer kumulierten Häufigkeitstabelle (ohne Klassierung) zusammen.
b) Berechnen Sie das arithmetische Mittel.
Arithmetisches Mittel bei klassierten Daten
Eine Gruppe von 50 Studierenden wird nach ihrem ungefähren Lernaufwand für eine Statistikklausur (in Tagen) befragt. Es ergeben sich die folgenden (klassierten) Werte:
a) Füllen Sie den Rest der kumulierten Häufigkeitstabelle aus.
b) Berechnen Sie das arithmetische Mittel.
Getrimmtes arithmetisches Mittel
Eine Gruppe von Studierenden befragt Passantinnen und Passanten auf dem Campus. Erhoben wird dabei unter anderem das Alter (in Jahren). Hierfür ergeben sich für 20 Personen folgende Werte:
a) Berechnen Sie das um 5% getrimmte arithmetische Mittel.
b) Berechnen Sie das um 10% getrimmte arithmetische Mittel.
Lösungen der Übungsaufgaben
Arithmetisches Mittel
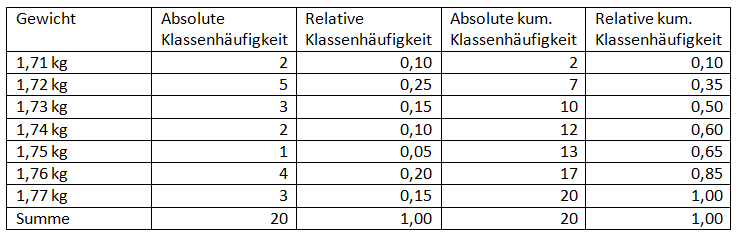
Aus einem Produktionslos von 1.000 Karosserieteilen wird eine Stichprobe von 20 Teilen gezogen und gewogen. Es ergeben sich die folgenden Werte:
a) Fassen Sie diese Werte in einer kumulierten Häufigkeitstabelle (ohne Klassierung) zusammen.
b) Berechnen Sie das arithmetische Mittel.
(1,71 * 2) + (1,72 * 5) + (1,73 * 3) + (1,74 * 2 ) + (1,75 * 1) + (1,76 * 4) + (1,77 * 3) = 34,79
34,79 / 20 = 1,7395
Das arithmetische Mittel liegt bei 1,7395 kg.
Arithmetisches Mittel bei klassierten Daten
Eine Gruppe von 50 Studierenden wird nach ihrem ungefähren Lernaufwand für eine Statistikklausur (in Tagen) befragt. Es ergeben sich die folgenden (klassierten) Werte:
a) Füllen Sie den Rest der kumulierten Häufigkeitstabelle aus.
b) Berechnen Sie das arithmetische Mittel.
(2 * 0,34) + (4 * 0,46) + (6 * 0,20) = 0,68 + 1,84 + 1,20 = 3,72
Das arithmetische Mittel beträgt 3,72 Tage.
Getrimmtes arithmetisches Mittel
Eine Gruppe von Studierenden befragt Passantinnen und Passanten auf dem Campus. Erhoben wird dabei unter anderem das Alter (in Jahren). Hierfür ergeben sich für 20 Personen folgende Werte:
a) Berechnen Sie das um 5% getrimmte arithmetische Mittel.
20 * 0,05 = 1 -> Der Datensatz wird um je einen Wert an beiden Enden der Verteilung gekürzt.
12 + 19 + 21 + 21 + 22 + 23 + 23 + 23 + 23 + 24 + 26 + 27 + 27 + 28 + 30 + 31 + 34 + 37 = 451
451 / 18 = 25,06
Das um 5% getrimmte arithmetische Mittel liegt bei 25,06 Jahren.
b) Berechnen Sie das um 10% getrimmte arithmetische Mittel.
20 * 0,10 = 2 -> Der Datensatz wird um je zwei Werte an beiden Enden der Verteilung gekürzt.
19 + 21 + 21 + 22 + 23 + 23 + 23 + 23 + 24 + 26 + 27 + 27 + 28 + 30 + 31 + 34 = 402
402 / 16 = 25,125
Das um 10% getrimmte arithmetische Mittel liegt bei 25,125 Jahren.
Die hier vorgestellten Inhalte und Aufgaben sind Teil der Vorlesung “Grundlagen der Statistik” im berufsbegleitenden Bachelor-Studiengang Betriebswirtschaftslehre an der Hochschule Harz. Eine vollständige Übersicht aller Inhalte dieser Vorlesung im Wissenschafts-Thurm findet sich hier: Grundlagen der Statistik.