(Der Blog-Beitrag zu dieser Übung findet sich hier.)
Schiefe und Wölbung
Bei einer Fertigungsanlage werden 20 Polymerbauteile als Zufallsstichprobe aus der laufenden Produktion entnommen und gewogen. Die (absoluten) Abweichungen von einem Idealgewicht in Gramm werden in einer Tabelle festgehalten.
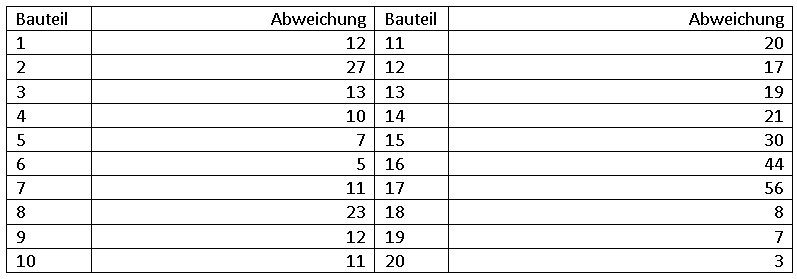
a) Berechnen Sie den Momentenkoeffizienten der Schiefe.
b) Berechnen Sie den Quartilskoeffizienten der Schiefe.
c) Berechnen Sie die Kurtosis.
Lösungen der Übungsaufgaben
Momentenkoeffizient der Schiefe
Zunächst wird die bereits bekannte Hilfstabelle mit zwei zusätzlichen Spalten angelegt.
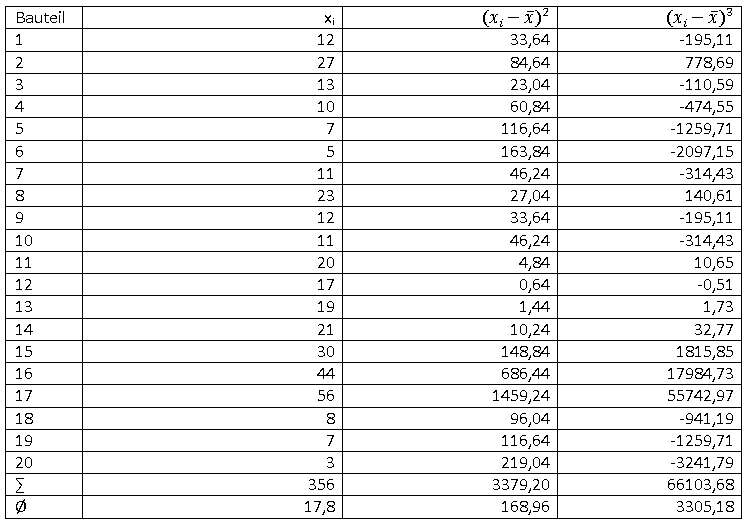
Auf Basis der tabellierten Werte ermittelt sich der Momentenkoeffizient der Schiefe wie folgt:
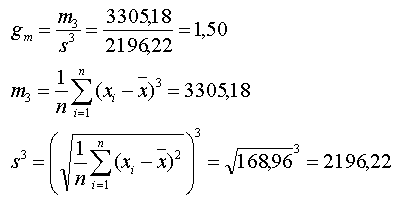
Der Momentenkoeffizient der Schiefe liegt bei 1,50 – die Verteilung ist somit linkssteil.
Quartilskoeffizient der Schiefe
Der Quartilskoeffizient der Schiefe berechnet sich aus den drei Quartilswerten.
Die geordnete Verteilung: 3; 5; 7; 7; 8; 10; 11; 11; 12; 12; 13; 17; 19; 20; 21; 23; 27; 30; 44; 56
Da (n * p) jeweils ganzzahlige Werte (k) ergibt, berechnen sich die Perzentile wie folgt:
(n*p) = (20 * 0,25) = 5 -> k = 5; k+1 = 6 -> x0,25 = (8+10)/2 = 9
(n*p) = (20 * 0,50) = 10 -> k = 10; k+1 = 11 -> x0,50 = (12+13)/2 = 12,5
(n*p) = (20 * 0,75) = 15 -> k = 15; k+1 = 16 -> x0,75 = (21+23)/2 = 22
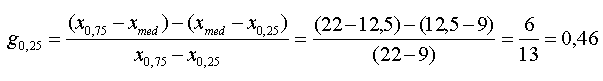
Auch hier ergibt sich ein positiver Wert – die Verteilung ist somit linkssteil.
Kurtosis
Auch für die Berechnung der Kurtosis wird zunächst eine Hilfstabelle angelegt.
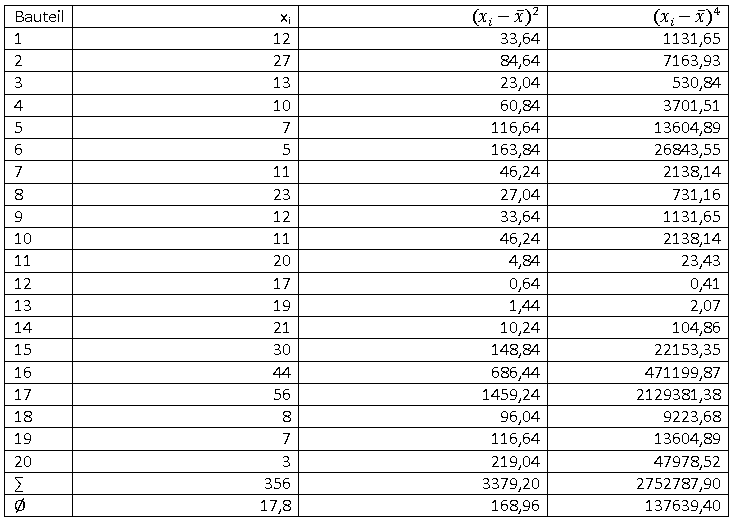
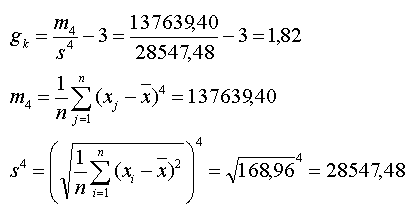
Der positive Wert der Kurtosis weist auf einen im Vergleich zur Wölbung der Normalverteilung spitzeren Verlauf der Verteilung hin.
Die hier vorgestellten Inhalte und Aufgaben sind Teil der Vorlesung “Grundlagen der Statistik” im berufsbegleitenden Bachelor-Studiengang Betriebswirtschaftslehre an der Hochschule Harz. Eine vollständige Übersicht aller Inhalte dieser Vorlesung im Wissenschafts-Thurm findet sich hier: Grundlagen der Statistik.
