Übungsaufgaben mit Musterlösungen zur Statistik: Box-Plot-Konstruktion

(Der Blog-Beitrag zu dieser Übung findet sich hier.)

Box-Plot

Auf dem Campus der Hochschule Harz wurden 20 willkürlich ausgewählte Professorinnen und Professoren nach ihrem Alter befragt. Dabei ergab sich folgendes Bild:

Beispiel Box-Plot

1) Konstruieren Sie einen erweiterten Box-Plot.

Lösung der Übungsaufgabe

Zur Berechnung der Quartile ordnen wir im ersten Schritt die Werte der Verteilung:

33; 39; 40; 42; 44; 44; 45; 46; 48; 50; 51; 52; 53; 54; 55; 56; 60; 61; 62; 66

Da (n * p) jeweils ganzzahlige Werte (k) ergibt, berechnen sich die Quartile wie folgt:

(n*p) = (20 * 0,25) = 5 -> k = 5; k+1 = 6 -> x_p = (44+44)/2=44
(n*p) = (20 * 0,50) = 10 -> k = 10; k+1 = 11 -> x_p = (50+51)/2=50,5
(n*p) = (20 * 0,75) = 15 -> k = 15; k+1 = 16 -> x_p = (55+56)/2=55,5

Weiterhin sind der IQR sowie der 1,5- und 3-fache IQR zu bestimmen:

IQR = 55,5 – 44 = 11,5
1,5 IQR = 17,25
3,0 IQR = 34,50

Auf Basis dieser Ergebnisse lässt sich der Box-Plot nun wie gewohnt konstruieren:

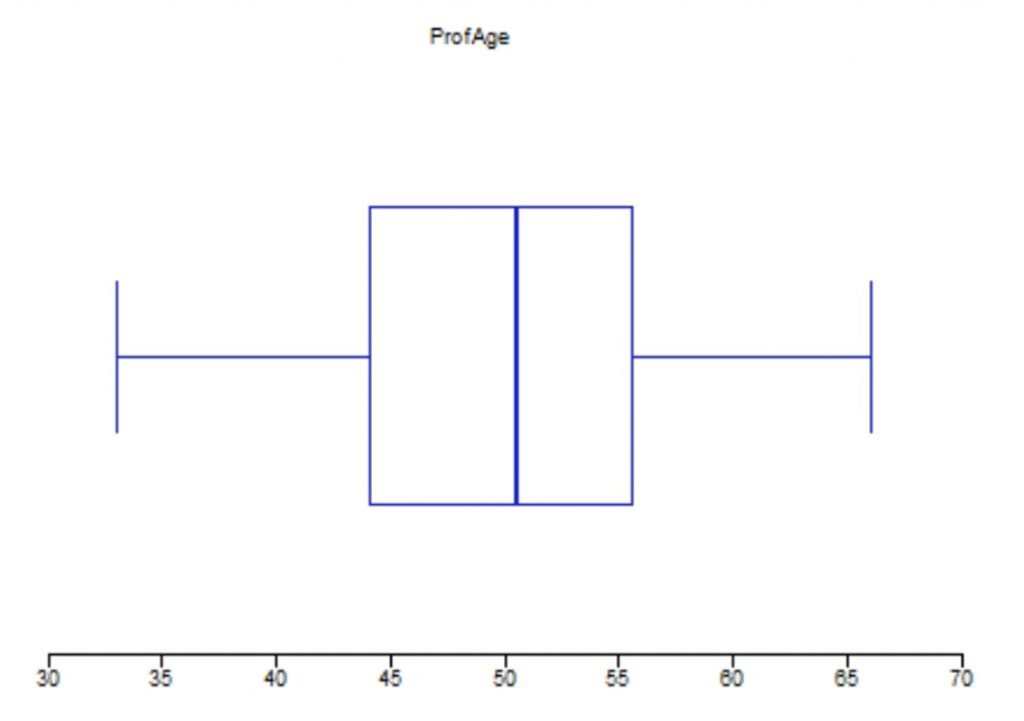
Die Box verläuft von 44 (unteres Quartil) bis zu 55,5 (oberes Quartil).
Der Median (mittleres Quartil) wird in diese Box beim Wert 50,5 eingezeichnet.
Der obere Zaun könnte maximal bis zum Wert 55,5 + 17,25 = 72,75 reichen. Der größte in dem Bereich liegende Wert (und damit die Grenze des oberen Zauns) ist die 66. Da sich im Datensatz keine größeren Werte befinden, gibt es nach oben keine Ausreißer.
Der untere Zaun könnte minimal bis zum Wert 44 – 17,25 = 26,75 reichen. Der kleinste in diesem Bereich liegende Wert (und damit die Grenze des unteren Zauns) ist die 33. Da sich im Datensatz keine kleineren Werte befinden, gibt es auch nach unten keine Ausreißer.
Zu Übungszwecken sei an dieser Stelle noch aufgeführt, dass Ausreißer nach oben zwischen 72,75 und (einschließlich) 90, Ausreißer nach unten zwischen 26,75 und (einschließlich) 9,5 hätten liegen müssen. Werte oberhalb von 90 bzw. unterhalb von 9,5 hätten dagegen als Extremwerte gekennzeichnet werden müssen.

Die Kontrollgrafik wurde hier nicht mit PAST, sondern mit SSP (seitlich liegend) erstellt.

Box-Plot Altersverteilung

Die hier vorgestellten Inhalte und Aufgaben sind Teil der Vorlesung “Grundlagen der Statistik” im berufsbegleitenden Bachelor-Studiengang Betriebswirtschaftslehre an der Hochschule Harz. Eine vollständige Übersicht aller Inhalte dieser Vorlesung im Wissenschafts-Thurm findet sich hier: Grundlagen der Statistik.