AUFGABE
Die nachfolgende Tabelle enthält zehn Datensätze aus einer Studierendenbefragung, die auf dem Campus der Hochschule Harz durchgeführt wurde. Gefragt wurde (unter anderem) nach Alter, (biologischem) Geschlecht, monatlich verfügbarem Nettoeinkommen und gewähltem Studiengang.
| Nr. | Alter | Geschlecht | Einkommen | Studiengang |
| 1 | 21 Jahre | männlich | 580,00 EUR | BWL |
| 2 | 20 Jahre | männlich | 420,00 EUR | BWL |
| 3 | 23 Jahre | weiblich | 230,00 EUR | Informatik |
| 4 | 28 Jahre | männlich | 450,00 EUR | Medienkonzeption |
| 5 | 20 Jahre | weiblich | 380,00 EUR | Medienkonzeption |
| 6 | 27 Jahre | weiblich | 450,00 EUR | Informatik |
| 7 | 33 Jahre | männlich | 320,00 EUR | Informatik |
| 8 | 21 Jahre | weiblich | 410,00 EUR | BWL |
| 9 | 22 Jahre | weiblich | 280,00 EUR | BWL |
| 10 | 19 Jahre | weiblich | 260,00 EUR | Medienkonzeption |
Zeichen Sie einen erweiterten Box-Plot für das Alter und geben Sie die für die Konstruktion erforderlichen Größen an. Wie alt müsste ein zusätzlicher (!) Proband mindestens (!) sein, um im Box-Plot als Ausreißer am oberen Rand der Verteilung ausgewiesen zu werden?
Der für die Lösung dieser Aufgabe erforderliche theoretische Hintergrund lässt sich hier noch einmal nachlesen. Die Musterlösung findet sich dann unterhalb des Pfeils.
 MUSTERLÖSUNG
MUSTERLÖSUNG
Vorbereitender Schritt: Ordnen der Werte
| Wert | 19 | 20 | 20 | 21 | 21 | 22 | 23 | 27 | 28 | 33 |
| Stelle | 1. | 2. | 3. | 4. | 5. | 6 | 7. | 8. | 9. | 10. |
Erster Schritt: Konstruktion der Box mittels der Quartile
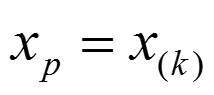 (wenn n * p keinen ganzzahligen Wert ergibt)
(wenn n * p keinen ganzzahligen Wert ergibt)
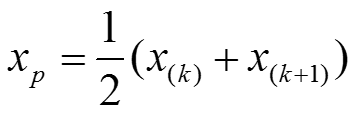 (wenn n * p einen ganzzahligen Wert ergibt)
(wenn n * p einen ganzzahligen Wert ergibt)
Unteres Quartil: 0,25 * 10 = 2,5 -> Wert an 3. Stelle der geordneten Verteilung -> 20
Mittleres Quartil bzw. Median: 0,50 * 10 = 5 -> Mittel aus den beiden Werten an 5. und 6. Stelle der geordneten Verteilung -> (21 + 22) / 2 = 21,5
Oberes Quartil: 0,75 * 10 = 7,5 -> Wert an 8. Stelle der geordneten Verteilung -> 27
Interquartilsabstand (IQR): 27 – 20 = 7
Die Box verläuft somit von 20 auf 27, der Median wird bei 21,5 eingezeichnet.
Zweiter Schritt: Konstruktion der Zäune mittels IQR
1,5-facher Interquartilsabstand (IQR): 7 * 1,5 = 10,5
Der untere Zaun läuft minimal bis: 20 – 10,5 = 9,5
-> kleinster Wert in diesem Wertebereich ist die 19
Der obere Zaun läuft maximal bis: 27 + 10,5 = 37,5
-> größter Wert in diesem Wertebereich ist die 33
Der untere Zaun läuft somit bis zur 19, der obere Zaun bis zur 33.
Dritter Schritt: Identifikation der Ausreißer mittels IQR
(entfällt, da die Zäune bereits den größten und kleinsten Wert im Datensatz einschließen)

Wie alt müsste ein zusätzlicher Proband sein, um als Ausreißer gewertet zu werden?
Die simple Antwort ohne Ergänzung der Verteilung lautet: Mindestens 38 Jahre.
Für die komplexe (und bessere) Antwort ist zu berücksichtigen, dass die Ergänzung des Datensatzes um einen weiteren Probanden hohen Alters die Neuberechnung des IQR sowie der maximalen Grenze des oberen Zauns erforderlich macht. Dabei spielt es aufgrund der Robustheit der für die Konstruktion des Box-Plots verwendeten Kennzahlen keine Rolle, welchen konkreten Wert man diesem Ausreißer zuweist. Diese Neubestimmung ergibt:
Unteres Quartil: 0,25 * 11 = 2,75 -> Wert an 3. Stelle der geordneten Verteilung -> 20
Oberes Quartil: 0,75 * 11 = 8,25 -> Wert an 9. Stelle der geordneten Verteilung -> 28
Interquartilsabstand (IQR): 28 – 20 = 8
1,5-facher IQR = 1,5 * 8 = 12
Der obere Zaun läuft somit maximal bis 28 + 12 = 40.
Ein Ausreißer müsste also mindestens 41 Jahre alt sein (wenn nur vollendete Lebensjahre angegeben werden).
>>> Zurück zur Übersichtsseite Statistik.
Diese Übungsaufgabe stammt aus der Vorlesung “Grundlagen der Statistik” von Christian Reinboth im berufsbegleitenden Bachelor-Studiengang BWL an der Hochschule Harz.
