Liegen metrisch skalierte Daten (natürlich bei beiden Variablen) vor, kann – wie im letzten Blogpost erläutert – der Korrelationskoeffizient nach Bravais-Pearson berechnet werden. Dieser ist aber ausschließlich ein Maß für die Stärke einer linearen Korrelation zwischen zwei Variablen. Liegt eine andere Form des Zusammenhangs – wie etwa ein quadratischer oder logarithmischer Zusammenhang – vor, wird dieser durch Bravais-Pearson nicht bzw. nicht vollumfänglich aufgedeckt. Bei der Interpretation des Korrelationskoeffizienten ist somit unbedingt zu berücksichtigen, dass ein niedriger Wert nicht bedeutet, dass zwischen den untersuchten Variablen keinerlei Zusammenhang besteht – er bedeutet lediglich, dass zwischen den untersuchten Variablen kein linearer Zusammenhang besteht.
Der Bravais-Pearson-Korrelationskoeffizient (der Einfachheit halber oft auch als BPK abgekürzt) wird anhand folgender Formel berechnet:
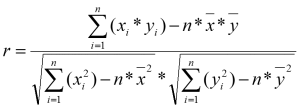
Die Formel lässt erkennen, dass für eine erleichterte Berechnung das Anlegen einer Hilfstabelle mit folgenden Spalten sinnvoll ist:
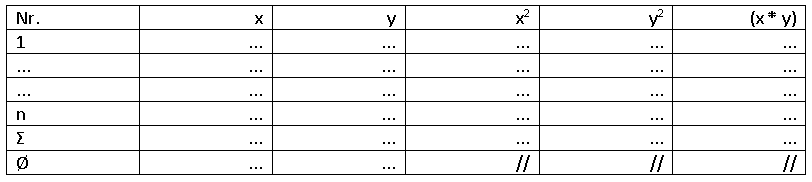
Der Korrelationskoeffizient r liegt stets zwischen -1 und +1 und wird wie folgt interpretiert:
- Bei positiven Werten liegt ein positiver Zusammenhang vor (die Wertepaare liegen auf einer steigenden Geraden), bei negativen Werten ein negativer Zusammenhang (die Wertepaare liegen auf einer fallenden Geraden). Werte nahe Null deuten darauf hin, dass zwischen den Variablen keine lineare Korrelation existiert.
- Liegt der Betrag (!) von r nahe 0, liegt keine (lineare) Korrelation vor, bei Werten bis 0,5 kann von einer schwachen, bei Werten zwischen 0,5 und 0,8 von einer mittelstarken und bei Werten zwischen 0,8 bis 1,0 von einer starken Korrelation gesprochen werden, wobei der maximal erreichbare Betrag von 1,0 eine perfekte Korrelation (alle Punkte liegen wie auf einer Perlenschnur genau auf einer Geraden) anzeigen würde. Die hier aufgezeigten Interpretationsgrenzen sind dabei nicht verbindlich, sondern stellen lediglich (erfahrungswertbasierte) Vorschläge dar.
Beispielrechnung
Ein Eishändler variiert ceteris paribus (unter sonst gleichbleibenden Rahmenbedingungen) die Preise einer Kugel Eis über den Verlauf von sieben Tagen und zeichnet auf, wie viele Kugeln zum jeweiligen Preis veräußert wurden.
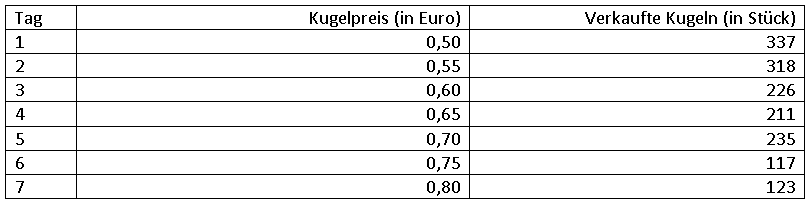
Berechnen Sie den Bravais-Pearson-Korrelationskoeffizienten.
Im ersten Schritt ist die bereits vorgestellte Hilfstabelle anzulegen und auszufüllen.
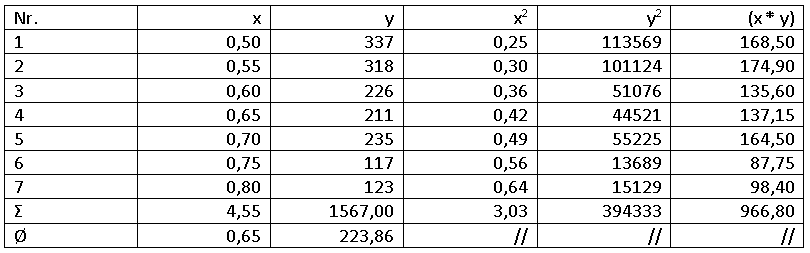
Die auf diese Weise errechneten Werte (zur Berechnung der beiden arithmetischen Mittel für die Variablen x und y siehe diesen Blogpost) werden anschließend in die Formel eingesetzt.
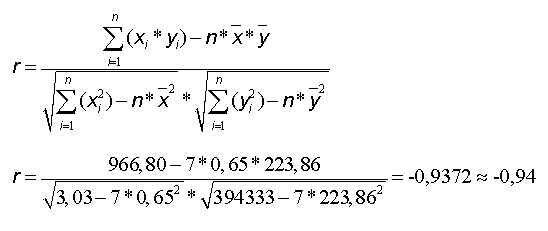
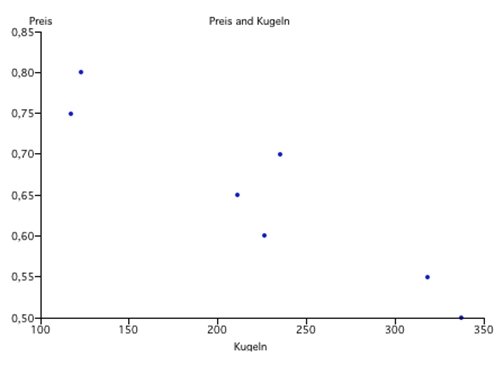
Das Ergebnis weist auf eine starke negative Korrelation zwischen beiden Variablen hin – ein Ergebnis, das durch einen Blick auf das Streudiagramm (im Beispiel erstellt mit SSP) bestätigt wird.
Übungsaufgabe
Eine Hochschule befragt zehn Absolventen/innen fünf Jahre nach ihrem Abschluss nach ihrem aktuellen Nettogehalt und ordnet die Summen den (metrisch skalierten!) Punkten in ihrer Abschlussklausur zu. Existiert eine lineare Korrelation zwischen dem Abschneiden in der Klausur und dem Nettogehalt nach fünf Jahren Berufstätigkeit?

1) Berechnen und interpretieren Sie den Bravais-Pearson-Korrelationskoeffizienten.
Zur Anzeige der Lösungen bitte hier klicken.
Die hier vorgestellten Inhalte und Aufgaben sind Teil der Vorlesung “Grundlagen der Statistik” im berufsbegleitenden Bachelor-Studiengang Betriebswirtschaftslehre an der Hochschule Harz. Eine vollständige Übersicht aller Inhalte dieser Vorlesung im Wissenschafts-Thurm findet sich hier: Grundlagen der Statistik.

