Angenommen, es existiere ein Test auf das Vorhandensein eines genetischen Merkmals, das im hohen Alter eine bestimmte schwere Erkrankung auslöst. Dieser Test identifiziert das Merkmal, das bei 5% der Bevölkerung auftritt, mit einer Sicherheit von 95%. Im Rahmen einer Massenuntersuchung werden 100.000 Personen getestet. Wie groß ist nun die Wahrscheinlichkeit dafür, dass eine als Träger des Merkmals identifizierte Person wirklich über das Merkmal verfügt? Die meisten Menschen würden diese Frage spontan mit 95% beantworten – schließlich ist ja der Test zu 95% sicher, also wird es auch das Ergebnis sein. Der Irrtum, dem wir dabei kollektiv unterliegen, ist die völlige Vernachlässigung der Wahrscheinlichkeit dafür, dass das (mit 5% ja eher seltene) Merkmal überhaupt bei dieser Testperson vorliegt.
Die reale Wahrscheinlichkeit für einen Treffer erschließt man sich am besten durch die Betrachtung der absoluten Häufigkeiten:
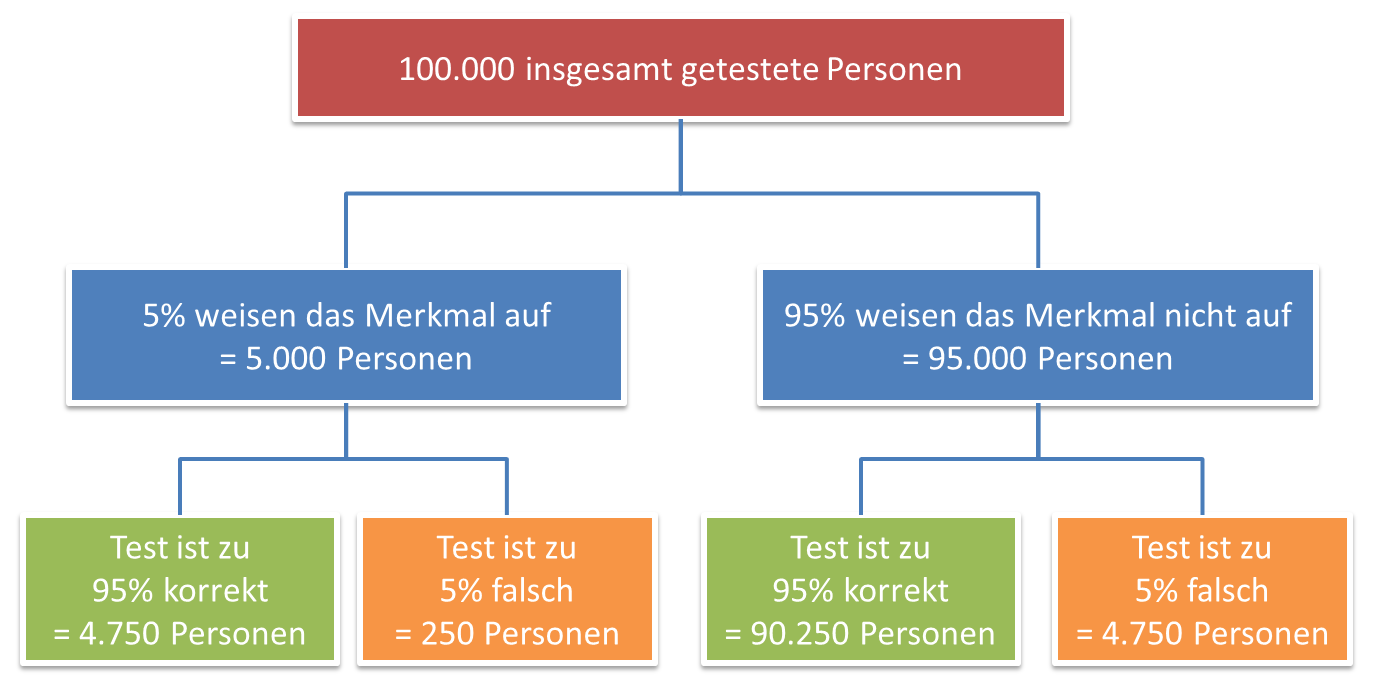
Von 100.000 Testpersonen verfügen 5% wirklich über das Merkmal – das sind 5.000 Personen. Von diesen 5.000 Personen werden – da der Test zu 95% sicher ist – insgesamt 4.750 Personen korrekterweise als Merkmalsträger erkannt. Da der Test, wenn er zu 95% sicher ist, auch mit 5% irrt, werden von den 95.000 gesunden Testpersonen allerdings auch 5% – dies entspricht ebenfalls 4.750 Personen – fälschlicherweise als Merkmalsträger eingestuft. Alles in allem sind den Testergebnissen zufolge also 4.750 + 4.750 = 9.500 Personen Merkmalsträger, von denen allerdings nur 4.750 Personen (50%) wirklich das Merkmal aufweisen. Die Wahrscheinlichkeit dafür, dass eine Person wirklich das Merkmal aufweist, wenn der Test sie als Merkmalsträger identifiziert, liegt somit nur bei 50% – auch wenn der Test selbst zu 95% sicher ist.
Die tatsächliche Wahrscheinlichkeit errechnet sich also dadurch, dass man entsprechend der klassischen Wahrscheinlichkeitsdefinition nach Laplace die Summe der für das betrachtete Ergebnis relevanten Fälle (Testpersonen mit Merkmal, bei denen das Merkmal diagnostiziert wurde) zu allen Fällen (Testpersonen mit oder ohne Merkmal, bei denen das Merkmal diagnostiziert wurde) in Beziehung setzt. Der Ersatz der absoluten Werte durch die Wahrscheinlichkeiten – unter Berücksichtigung von Additions- und Multiplikationssatz – führt zum gleichen Ergebnis: (0,05*0,95) / ((0,05*0,95) + (0,95*0,05)) = 0,50.
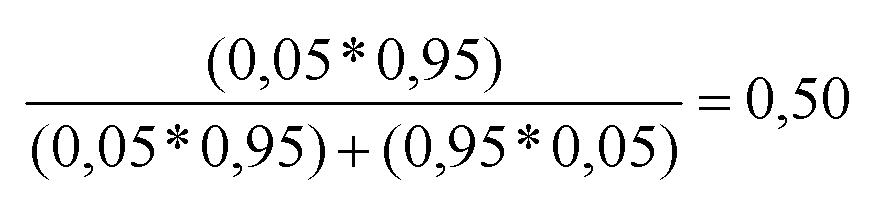
Aus dieser Überlegung lässt sich der sowohl für das Verständnis der Wahrscheinlichkeitslehre als auch vieler Alltagsprobleme hochgeradig relevante Satz von Bayes ableiten:
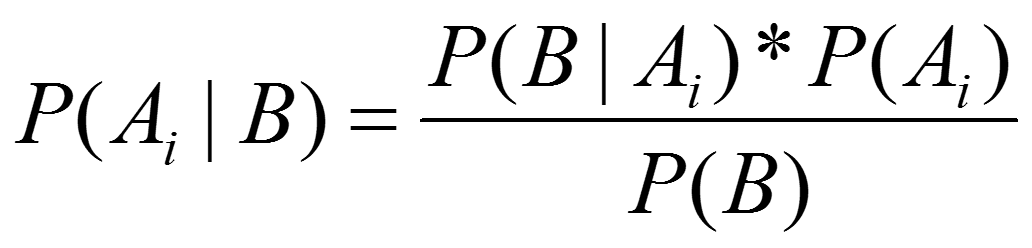
Wie aber ist diese Formel richtig zu lesen?
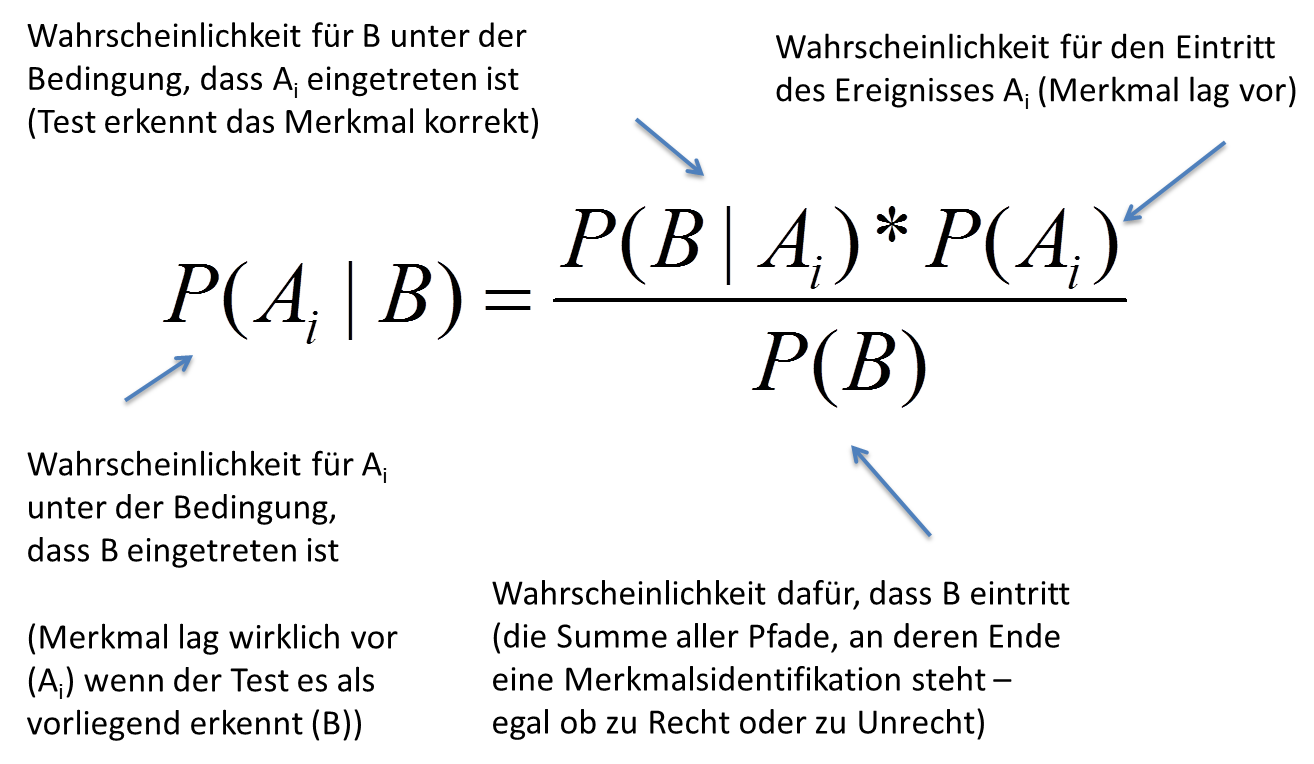
Eine Darstellung des “berühmtesten” Beispiels zum Satz von Bayes – des sogenannten Taxi-Problems des deutschen Mathematikers Arthur Engel – findet sich übrigens hier in meinem Blog auf ScienceBlogs.de.
Beispielrechnung
Eine Hochschule prüft sämtlich eingereichten Bachelor-Arbeiten mit einer eigens entwickelten Software auf Plagiate. Diese werden von der Software mit einer Sicherheit von 95% korrekt erkannt. Jedes Semester reichen 800 Studierende an dieser Hochschule Bachelor-Arbeiten zur Kontrolle ein, wobei leider davon auszugehen ist, dass in 3% der eingereichten Arbeiten Plagiate enthalten sind.
Wie groß ist die Wahrscheinlichkeit dafür, dass eine durch die Software als plagiatsverdächtig identifizierte Arbeit auch tatsächlich ein Plagiat enthält?
Von 800 eingereichten Bachelor-Arbeiten enthalten…
… 776 keine Plagiate (97%)
… 24 Plagiate (3%)
Von 776 Arbeiten ohne Plagiate…
… werden 737,2 korrekterweise als sauber klassifiziert (95%)
… werden 38,8 fälschlicherweise als unsauber klassifiziert (5%)
Von 24 Arbeiten mit Plagiaten…
… werden 22,8 korrekterweise als unsauber klassifiziert (95%)
… werden 1,2 fälschlicherweise als sauber klassifiziert (5%)
Insgesamt werden also 38,8 + 22,8 = 61,6 Arbeiten als Plagiate eingestuft. Von diesen 61,6 Arbeiten sind aber nur 22,8 Arbeiten wirklich Plagiate. Die Wahrscheinlichkeit dafür, dass eine als plagiatsverdächtig eingestufte Arbeit auch tatsächlich ein Plagiat enthält, liegt somit bei lediglich 37,01%.
Übungsaufgaben
Eine Sicherheitssoftware für die Analyse von Videoaufnahmen an einer Flughafen-Sicherheitsschleuse kann das Gesicht von gesuchten Personen mit einer Wahrscheinlichkeit von 92% erkennen. Allerdings identifiziert die Software in 3% aller Fälle eine nicht gesuchte Person irrtümlich als gesucht. Die Sicherheitsbehörden gehen davon aus, dass an einem bestimmten Tag eine Gruppe von 10 gesuchten Personen versuchen wird, die Schleuse zu passieren. Das Personenaufkommen pro Tag liegt bei 10.000 Fluggästen. Mit der Präsenz weiterer gesuchter Personen ist am betrachteten Tag nicht zu rechnen.
a) Mit wie vielen fälschlicherweise als “gesucht” identifizierten Personen ist zu rechnen?
b) Die Software schlägt Alarm. Wie groß ist die Wahrscheinlichkeit dafür, dass tatsächlich eine gesuchte Person entdeckt wurde?
Zur Anzeige der Lösungen bitte hier klicken.
Die hier vorgestellten Inhalte und Aufgaben sind Teil der Vorlesung “Grundlagen der Statistik” im berufsbegleitenden Bachelor-Studiengang Betriebswirtschaftslehre an der Hochschule Harz. Eine vollständige Übersicht aller Inhalte dieser Vorlesung im Wissenschafts-Thurm findet sich hier: Grundlagen der Statistik.



Hier wird in allen Beispielen davon ausgegangen, dass ein false positive genauso wahrscheinlich ist, wie ein false negative. Das ist aber sicherlich nicht oder nur selten der Fall. Insofern müsste man P(B) differenzierter betrachten….
@Knut: Das ist in der Tat vereinfachend und didaktisch möglicherweise unklug – in vielen meiner Übungsaufgaben laufen false positives und false negatives aber durchaus auseinander, nur eben nicht in der hier zusammengestellten Auswahl. Wenn aus dem Skript hier irgendwann mal ein Buch wird, werde ich darauf achten, dass die Wahrscheinlichkeiten bei mindestens einer Übungsaufgabe nicht identisch sind – vielen Dank für den Hinweis.