Neben den Maßen der zentralen Tendenz (Zentrum einer Verteilung) und den Dispersionsparametern (Streuung der Werte einer Verteilung um dieses Zentrum), lassen sich Verteilungen auch – wenn dies auch weniger gebräuchlich ist – über ihre Form charakterisieren. Dies kann über die Schiefe (linkssteil/rechtsschief, rechtssteil/linksschief oder symmetrisch) sowie über die Wölbung (ähnlich der Wölbung einer Normalverteilung, spitzer als die einer Normalverteilung oder flacher als die einer Normalverteilung) geschehen. Die Schiefe kann über den Momentenkoeffizienten oder über den Quartilskoeffizienten der Schiefe, die Wölbung über die Kurtosis / Exzeß bestimmt werden.
Momentenkoeffizient der Schiefe
Die Berechnung des Momentenkoeffizienten der Schiefe basiert auf der bereits bekannten Formel für die Berechnung der Varianz (quadrierte durchschnittliche Abweichung der Werte einer Verteilung von deren arithmetischem Mittel). Da die Berechnung des Momentenkoeffizienten die Berechnung des arithmetischen Mittels voraussetzt, kann dieser nur für metrische Daten ermittelt werden. Für die Berechnung des Momentenkoeffizienten gm werden drei Formeln benötigt:

Liegt der Momentenkoeffizient der Schiefe nahe Null, handelt es sich um eine symmetrische Verteilung. Positive Werte deuten dagegen auf eine linkssteile, negative auf eine rechtssteile Verteilung hin. Wer die Formel für s³ näher betrachtet, wird feststellen, dass es sich um die Formel für die Varianz handelt, aus der die Wurzel gezogen (ergibt die Standardabweichung) und die anschließend mit 3 potenziert wird. Bei s³ handelt es sich also um die dritte Potenz der Standardabweichung s.
Quartilskoeffizient der Schiefe
Liegen lediglich ordinalskalierte Daten vor, kann der Momentenkoeffizient der Schiefe nicht berechnet werden. Möglich ist in diesem Fall allerdings die Berechnung des Quartilskoeffizienten der Schiefe, der anstelle des arithmetischen Mittels auf die ebenfalls bereits bekannten Quartile aufbaut.

Die Interpretation des Quartilskoeffizienten erfolgt analog zu der des Momentenkoeffizienten: Liegt der Wert nahe Null, handelt es sich um eine symmetrische Verteilung, während positive Werte auf eine linkssteile und negative Werte auf eine rechtssteile Verteilung hindeuten. Zu beachten ist außerdem: Beträgt der Interquartilsabstand (IQR, x0,75 – x0,25) Null, kann der Quartilskoeffizient der Schiefe nicht berechnet werden, da eine Division durch Null nicht möglich ist.
Kurtosis / Exzeß
Neben der Linkssteilheit/Rechtssteilheit von Verteilungen ist die Wölbung einer Verteilung ein weiteres interessantes Kriterium. Mit Hilfe der Kurtosis (auch als Exzeß bezeichnet), kann festgestellt werden, inwieweit die Wölbung einer Verteilung der Wölbung der bekannten Normalverteilung gleicht. Da die Formel voraussetzt, dass das arithmetische Mittel berechnet werden kann, lässt sich die Kurtosis – wie bereits der Momentenkoeffizient der Schiefe – nur dann berechnen, wenn metrisch skalierte Daten vorliegen.

Ergibt sich ein Wert nahe Null, entspricht die Wölbung der Verteilung der Wölbung einer Normalverteilung. Bei einem positiven Wort ist von einer „spitzeren“ Form der Verteilung, bei einem negativen Wert dagegen von einer „flacheren“ Form der Verteilung auszugehen. Die etwas deplatziert wirkende Subtraktion von 3 in der Hauptformel ist übrigens darauf zurückzuführen, dass die Normalverteilung eine Kurtosis von 3 aufweist – durch das Abziehen von 3 vom Ergebnis, ergibt sich bei völliger Gleichheit mit der Normalverteilung also ein Wert von Null und somit die Möglichkeit, das Ergebnis analog zum Momentenkoeffizienten der Schiefe zu interpretieren.
Ebenso wie beim Momentenkoeffizienten der Schiefe ist die Interpretation der Kurtosis nur dann sinnvoll, wenn eine unimodale Verteilung vorliegt – und ebenso wie beim Momentenkoeffizienten findet sich auch hier in der Formel für s4 die Varianz bzw. die Standardabweichung wieder, die hier anstelle mit 3 mit 4 potenziert wird. Für Klausuren mit engem Zeitbudget interessant: Wurden Varianz und Standardabweichung für die vorliegenden Daten bereits berechnet, lässt sich die Berechnung des Momentenkoeffizienten sowie der Kurtosis also durch Rückgriff auf die Standardabweichung abkürzen.
Beispielrechnungen
An einer Fertigungsanlage werden 20 Polymerbauteile als Zufallsstichprobe aus der laufenden Produktion entnommen und gewogen. Die (absoluten) Abweichungen von einem avisierten Idealgewicht in Gramm werden in einer Tabelle festgehalten.

Berechnung des Momentenkoeffizienten
Ein Blick auf die Formeln verrät, dass eine Hilfstabelle zu Berechnung dreier Werte (arithmetisches Mittel von x, m3, s³) erforderlich ist.

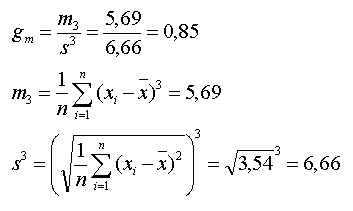
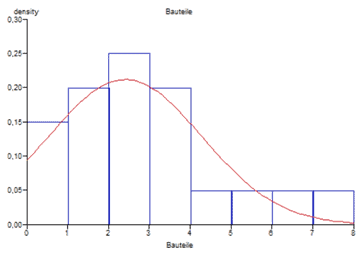
Der Momentenkoeffizient der Schiefe liegt bei 0,85 – die Verteilung ist somit leicht linkssteil. Ein Blick auf die Verteilungskurve (erstellt mit Smith’s Statistical Package) bestätigt diese Interpretation.
Berechnung des Quartilskoeffizienten
Der Quartilskoeffizient der Schiefe berechnet sich aus den drei Quartilswerten. Zu deren Bestimmung sind zunächst alle Werte der Verteilung in eine geordnete Reihe zu bringen. Hierbei ergibt sich:
0; 0; 0; 1; 1; 1; 1; 2; 2; 2; 2; 2; 3; 3; 3; 3; 4; 5; 6; 7
Da (n * p) in allen drei Fällen einen ganzzahligen Wert (k) ergibt, berechnen sich die Perzentile wie folgt:
(n*p) = (20 * 0,25) = 5 -> k = 5; k+1 = 6 -> x0,25 = (1+1)/2 = 1
(n*p) = (20 * 0,50) = 10 -> k = 10; k+1 = 11 -> x0,50 = (2+2)/2 = 2
(n*p) = (20 * 0,75) = 15 -> k = 15; k+1 = 16 -> x0,75 = (3+3)/2 = 3
Eingesetzt in die Formel für den Quartilskoeffizienten ergibt sich:

Der Quartilskoeffizient der Schiefe beträgt somit 0. Dies legt eine symmetrische Verteilung nahe und scheint zunächst im Widerspruch zum Momentenkoeffizient der Schiefe zu stehen. Tatsächlich lässt die Kurve aber beide Interpretationen zu – ein Beispiel, das verdeutlicht, wie problematisch bisweilen die Interpretation ohne fest definierte Grenzwerte sein kann.
Berechnung der Kurtosis
Auch für die Berechnung der Kurtosis empfiehlt sich die Anlage einer Hilfstabelle.


Die Kurtosis liegt mit 0,13 nahe der Null – damit ist die Wölbung ähnlich der einer Normalverteilung. Auch diese Annahme lässt sich durch die Betrachtung einer mit SSP erstellten Kurve bestätigen.
Übungsaufgaben
Der gleichen Fertigungsanlage werden erneut 20 Polymerbauteile als Zufallsstichprobe aus der laufenden Produktion entnommen und gewogen. Die diesmal deutlich größer ausfallenden (absoluten) Abweichungen von einem Idealgewicht in Gramm werden in einer Tabelle festgehalten.
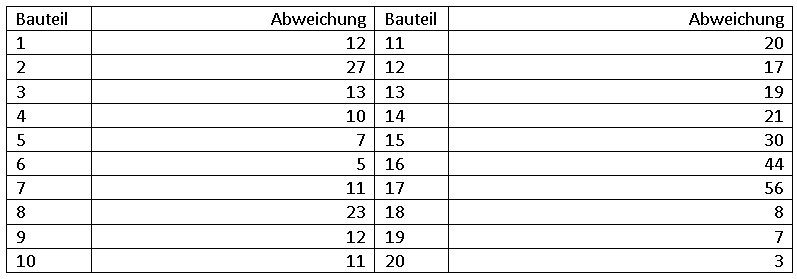
a) Berechnen Sie den Momentenkoeffizienten der Schiefe.
b) Berechnen Sie den Quartilskoeffizienten der Schiefe.
c) Berechnen Sie die Kurtosis.
Zur Anzeige der Lösungen bitte hier klicken.
Die hier vorgestellten Inhalte und Aufgaben sind Teil der Vorlesung “Grundlagen der Statistik” im berufsbegleitenden Bachelor-Studiengang Betriebswirtschaftslehre an der Hochschule Harz. Eine vollständige Übersicht aller Inhalte dieser Vorlesung im Wissenschafts-Thurm findet sich hier: Grundlagen der Statistik.

