Nehmen wir einmal an, uns lägen von einer Untersuchung der Wassertiefe an einem Deich genau zwei Merkmalswerte vor: Die Wassertiefe (1,85 m) sowie die Haarfarbe der Person, welche die Messung vorgenommen hat (blond). Intuitiv wird uns klar sein, dass sich mit dem Wert für die Wassertiefe deutlich mehr anfangen lässt, als mit der Angabe der Haarfarbe. So könnte man den Wert etwa mit dem einer vorherigen Messung vergleichen und berechnen, um wie viel Prozent der Wasserstand gefallen oder gestiegen ist. Kalkulieren könnte man auch die Differenz zur Höhe des Deichs und damit die Höhe, um die das Wasser noch steigen könnte, bevor eine kritische Marke erreicht wird. Im Hinblick auf die Haarfarbe könnten wir dagegen lediglich einen Vergleich mit den Aufzeichnungen früherer Messungen anstellen und ermitteln, ob die Prüfer stets blond waren, oder ob auch andere Haarfarben vertreten sind.
Der Informationsgehalt des Merkmals “Wassertiefe in m” ist offenbar deutlich größer als der Informationsgehalt des Merkmals “Haarfarbe”. Diese zentrale Eigenschaft von Merkmalen bzw. Variablen wird in der Statistik als deren Skalenniveau bezeichnet. Da die Durchführbarkeit einer Vielzahl von Analysen direkt oder indirekt davon abhängig ist, dass die vorhandenen Daten ein bestimmtes Skalenniveau erreichen, ist dessen fehlerfreie Bestimmung eine unerlässliche Voraussetzung für die Anwendung dieser Verfahren. Für die Zwecke unserer Statistik-Blogserie hier im “Wissenschafts-Thurm” wird eine Unterscheidung in die nachfolgend dargestellten drei Skalenniveaus ausreichend sein.
Nominalskalenniveau
Bei nominalskalierten Daten handelt es sich um Daten, die in keinerlei natürliche Reihenfolge gebracht werden können – beispielsweise um das Geschlecht, die Haarfarbe oder die Telefonnummer. Feststellbar ist hier lediglich, ob zwei statistische Einheiten im Hinblick auf ein nominalskaliertes Merkmal die gleichen Ausprägungen aufweisen – d.h. ob etwa beide befragten Personen blond sind oder ob sie über unterschiedliche Haarfarben verfügen. Da es sich beim Nominalskalennivau um dasjenige Skalenniveau mit dem geringsten Informationsgehalt handelt, lassen sich mit nominalskalierten Daten nur wenige Berechnungen anstellen – so kommt etwa als Lagemaß nur der Modus in Frage, während sich Streuung, Schiefe oder Wölbung einer nominalskalierten Verteilung gar nicht bestimmen lassen.
Beispiele: Geschlecht, Kontonummer, Haarfarbe, Telefonnummer, Geschmacksrichtung…
Ordinalskalenniveau
Im Gegensatz zu nominalskalierten Daten können ordinalskalierte Daten zwar in eine natürliche Reihenfolge gebracht werden – da allerdings die Abstände zwischen den einzelnen Werten nicht quantifizierbar sind, kann mit ihnen nicht “normal gerechnet” werden, obwohl es sich auf den ersten Blick um “normale Zahlen” handelt. Das klassische Beispiel hierfür sind Schulnoten. Schulnoten weisen sowohl eine natürliche Reihenfolge (eine 1 ist besser als eine 2, eine 2 ist besser als eine 3 usw.) als auch unterschiedliche Abstände zwischen den einzelnen Werten auf (der Notenbereich der 1 umfasst den Bereich von 92% bis 100% der maximal erreichbaren Punkte, der Notenbereich der 5 dagegen den Bereich von 0% bis 49%). Aus diesem Grund sind Rechenoperationen wie etwa das Addieren oder das Subtrahieren von Noten nicht sinnvoll: Zwei “2er” ergeben keinen “4er” – und wenn man von einem “2er” einen “1er” abzieht, erhält man auch keinen “3er”. Wenn man aber Schulnoten nicht addieren (oder dividieren) kann, folgt daraus auch, dass man beispielsweise kein arithmetisches Mittel aus ihnen bilden darf – auch wenn das leider an sehr vielen Schulen konsequent falsch praktiziert wird (und damit Generationen von Schülerinnen und Schülern für die Statistik verdorben werden).
Beispiele: Schulnoten, Präferenzrangfolgen, Zufriedenheit (z.B. auf einer Skala von 1 bis 5), militärische Dienstränge…
Metrisches Skalenniveau
Metrisch skalierte Daten verfügen über eine natürliche Reihenfolge sowie auch über quantifizierbare Abstände – mit ihnen kann also ganz “normal” gerechnet werden. In vielen Lehrbüchern wird innerhalb der metrischen Skala – die häufig auch als Kardinalskala bezeichnet wird – zusätzlich noch in die Intervallskala (ohne natürlichen Nullpunkt – z.B. Temperatur in Celsius) und in die Verhältnisskala (mit natürlichem Nullpunkt – z.B. Temperatur in Kelvin) unterschieden. Für die Zwecke unserer kleinen Blogserie wird diese Unterscheidung allerdings nicht von Bedeutung sein – hier reicht es vollkommen aus, metrisch skalierte Daten als solche korrekt erkennen zu können.
Beispiele: Zeitdauer in sek, Wassertiefe in cm, Preis in Euro und Cent, Streckenlänge in mm…
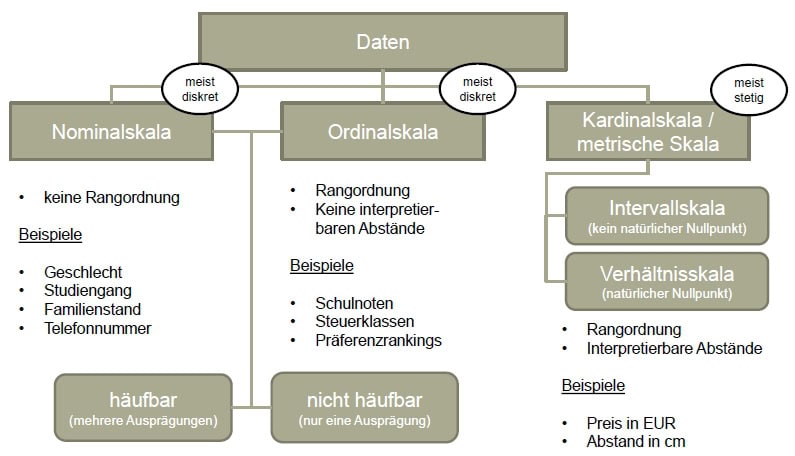
(Die Unterschiede zwischen diskreten und stetigen Daten sowie zwischen häufbaren und nicht häufbaren Merkmalen, werden wir dann übrigens in den nächsten Artikeln dieser Blogserie betrachten.)
Auf- und Abwärtskompatibilität
Für die im Rahmen unserer Blogserie betrachteten statistischen Verfahren gilt, dass sie im Hinblick auf das Skalenniveau – um an dieser Stelle einmal einen Begriff aus der Informatik zu bemühen – abwärtskompatibel, nicht aber aufwärtskompatibel sind. Dies bedeutet: Verfahren, die ein niedrigeres Skalenniveau voraussetzen, können stets auch auf Daten eines höheren Skalenniveaus angewandt werden – Verfahren, die ein höheres Skalenniveau voraussetzen, dürfen dagegen nie auf Daten eines niedrigeren Skalenniveaus angewandt werden. Da beispielsweise die Bestimmung des Modus lediglich voraussetzt, dass mindestens nominalskalierte Daten vorliegen, kann der Modus (wenn die übrigen Voraussetzungen erfüllt sind) auch für ordinalskalierte und metrische Daten bestimmt werden. Auf der anderen Seite kann etwa der Median, dessen Berechnung mindestens ordinalskalierte Daten voraussetzt, nicht für nominalskalierte Daten berechnet werden – die Berechnung für metrische Daten wäre dagegen problemlos möglich.
Der „Cheat Sheet“: Übersicht der Mindestskalenniveaus
An dieser Stelle greifen wir den in den nächsten Wochen noch folgenden Blogposts in einer kurzen Übersicht schon einmal ein wenig vor: Welches Skalenniveau muss mindestens erreicht werden, um eine Grafik erstellen oder eine Berechnung durchführen zu können?
1) Lagemaße / Maße der zentralen Tendenz
Modus: Nominalskala
Median: Ordinalskala
Quartile: Ordinalskala
Quantile: Ordinalskala
Perzentile: Ordinalskala
Arithmetisches Mittel: Kardinalskala
Geometrisches Mittel: Kardinalskala
Harmonisches Mittel: Kardinalskala
2) Streuungsmaße / Dispersionsparameter
Fünf-Werte-Zusammenfassung: Ordinalskala
Interquartilsabstand: Ordinalskala
Spannweite: Kardinalskala
Varianz: Kardinalskala
Standardabweichung: Kardinalskala
Variationskoeffizient: Kardinalskala
3) Verteilungsmaße / Schiefe und Wölbung
Quartilskoeffizient der Schiefe: Ordinalskala
Momentenkoeffizient der Schiefe: Kardinalskala
Kurtosis / Exzeß: Kardinalskala
4) Grafische Darstellungsformen
Venn-Diagramm: Nominalskala
Stamm-Blatt-Diagramm: Ordinalskala
(erweiterter) Box-Whisker-Plot: Ordinalskala
5) Zusammenhangsmaße
Chi²-Test auf stochastische Unabhängigkeit: Nominalskala
Rangkorrelationskoeffizient nach Spearman: Ordinalskala
Konkordanzkoeffizient nach Kendall: Ordinalskala
Bravais-Pearson-Korrelationskoeffizient: Kardinalskala
Die hier vorgestellten Inhalte und Aufgaben sind Teil der Vorlesung “Grundlagen der Statistik” im berufsbegleitenden Bachelor-Studiengang Betriebswirtschaftslehre an der Hochschule Harz. Eine vollständige Übersicht aller Inhalte dieser Vorlesung im Wissenschafts-Thurm findet sich hier: Grundlagen der Statistik.


Sehr interessant und anschaulich beschrieben, Christian. Allerdings verstehe ich noch nicht, warum ich von Schulnoten kein arithmetisches Mittel bilden darf. Nur weil ich diese nicht addieren oder subtrahieren kann? Für mich hat dieser Wert eine Aussagekraft. Er gibt an, welche Note im Durchschnitt über alle erreichten Noten erzielt wurde. Damit kann ich dann ermitteln, welche Note (Schüler, Student) besser oder schlechter als der Durchschnitt ist. Es werden doch sogar Verteilungsfunktionen ermittelt, um z.B. zu schauen, in wieweit die Notenverteilung mit der Normalverteilung übereinstimmt.
Das ist in der Tat genau der springende Punkt: Weil man ordinalskalierte Daten nicht addieren und auch nicht dividieren kann, kann man aus ihnen wirklich auch kein arithmetisches Mittel bilden, da dieses ja genau diese beiden Rechenschritte (erst alle Werte addieren, dann die Summe durch die Anzahl der Werte dividieren) voraussetzt. Dass der so berechnete Wert irgendwie richtig zu sein scheint bzw. sich “richtig anfühlt”, dürfte hauptsächlich daran liegen, dass sich aufgrund der Begrenztheit der Notenskala (nur Werte von 1 bis 5 bzw. von 1 bis 6) meist Werte ergeben, die (etwa im Gegensatz zum arithmetischen Mittel aus Telefonnummern) einen Sinn zu ergeben scheinen und die zudem nahe am rechnerisch tatsächlich möglichen Mittelwert – dem Median – liegen. Es bleibt aber trotzdem falsch – auch wenn es in der Praxis natürlich vielfach so gehandhabt wird (war in meiner Schule damals nicht anders).
Ein weiteres, ganz grundsätzliches Problem bei Schulnoten ist die Subjektivität der Notenvergabe. Dass es bei 80% der erreichbaren Punkte eine 2,0 gibt, sieht nur auf den ersten Blick nach einem objektiven Bewertungskriterium aus – denn wofür gibt es beispielsweise bei der Interpretation eines Gedichts (klar – bei Mathe geht das besser) am Ende Punkte oder Punktabzüge? Das kann bekanntlich nicht nur von Lehrer zu Lehrer, sondern durchaus auch von Schüler zu Schüler erheblich variieren. Die Behandlung von Schulnoten als kardinalskalierte Daten – gleichwertig mit beispielsweise einer gemessenen Wassertiefe in cm – unterstellt deshalb auch eine Objektivität und Vergleichbarkeit, die in der Praxis einfach nicht gegeben ist. Erwin Ebermann von der Uni Wien hat dazu in seinem Skript einiges geschrieben:
https://www.univie.ac.at/ksa/elearning/cp/quantitative/quantitative-52.html
Ich möchte anmerken, dass “gleichwertig mit beispielsweise einer gemessenen Wassertiefe in cm ” hier nicht trifft, da dies auf einer Ratio-Skala abgebildet werden kann (aufgrund des absoluten Nullpunktes). Einen solchen absoluten Nullpunkt gibt es bei Noten auf gar keinen Fall, weshalb diese allerhöchstens als intervalskaliert angesehen werden könnten (wie etwa die Temperatur in °C). “20°C ist doppelt so warm wie 10°C” ist unsinnig, “20 cm unter der Wasseroberfläche ist doppelt so tief wie 10cm” dagegen nicht.
Davon abgesehen sehe ich Schulnoten aber, wie Christian, als Ordinalskaliert an.
Völlig richtig – ein intervallskaliertes Beispiel wie Temperatur in °C wäre hier in der Tat besser geeignet gewesen. Auch an diesem Beispiel lassen sich die beiden wesentlichen Unterschiede zu Schulnoten ja aber gut darstellen:
1) Die Differenzen zwischen den einzelnen Messpunkten der Skala sind identisch, d.h. auch wenn “20 °C ist doppelt so warm wie 10 °C” eher weniger sinnvoll ist, so gilt doch, dass z.B ein Anstieg um 1 °C immer mit dem gleichen Sprung in der Skala verbunden ist, egal ob ich bei 5 °C oder bei 100 °C beginne – während der Sprung von einer 5,0 auf eine 4,0 im Hinblick auf direkt (Punkte) sowie indirekt (Leistung/Verständnis) gemessene Merkmale ein ganz anderer sein kann, als der von einer 2,0 auf eine 1,0.
2) Zehn Physiker*innen messen mit dem gleichen Thermometer im gleichen Raum zu gleichen Zeit zehn Mal die gleiche (oder zumindest fast gleiche) Temperatur. Zehn Lehrer*innen können das gleiche Essay zur Gretchenfrage in “Faust” zehn Mal völlig unterschiedlich bewerten – von der Problematik des Leistungsvergleiches bei unterschiedlichen Anforderungen (z.B. verschiedenen Fächern) noch ganz abgesehen…
Wie sollte man denn aus Ihrer Sicht bei der Mittelung von Schulnoten verfahren? Dies ist ja in verschiedenen Fällen erforderlich, z. B. wenn es darum geht eine Halbjahresgesamtnote für einen Schüler/eine Schülerin im Fach X zu ermitteln, die sich aus verschiedenen Einzelnoten von Klassenarbeiten und der mündlichen Note zusammensetzen soll – unter Umständen auch noch unterschiedlich gewichtet.
@Jan: Rein mathematisch betrachtet bietet sich für die Mittelung von Schulnoten der Median an, der aber wieder mit anderen Problemen verbunden ist: Schreibt ein Schüler bei vier von sieben Zwischenprüfungen eine 2 und bei drei von sieben eine 3, läge er bei einer Durchschnittsnote von 2, bei drei 2en und vier 3en dagegen bei einer 3, was wenig fair erscheint. Denkbar wäre auch Berechnung einer Note auf die durschnittliche prozentuale Bewertung der entsprechenden Prüfungen, sofern eine solche erfolgt: Würde ein Schüler bei drei Zwischenprüfungen jeweils 62%, 57% und 61% der möglichen Punkte erreichen, ließe sich das arithmetische Mittel der drei Werte (60%) errechnen und die für dieses Gesamtergebnis adäquate Note vergeben. Sofern eine Gewichtung erforderlich sein sollte, ließe sie sich in beide Kalkulation problemlos integrieren.
Ich hätte zwei Fragen bezüglich der Zuordnung zu einer Skala.
1) Handelt es sich bei Variablen mit Gruppen bei denen die Befragten keine genaue Angaben machen sondern sich zu bereits bestehenden Gruppen ordnen z.B. «Altersgruppen» des Typs 20-30, 21-30, 31-40 oder «Jahre der Berufstätigkeit» 0-5, 6-10, 11-15 u.s.w. um Ordinalskalierte? 2) Wird eine Variable z.B. Anzahl der Kinder: 0,1,2,…., >5 automatisch zu einer Ordinalskalierten wenn man sie Kategorien zuordnet (also 0=0, 1=1, 2=2, …,>5=6)
@TAMI: Vielen Dank für die beiden äußerst interessanten Fragen, an deren Beantwortung ich mich – ohne Gewähr – gerne versuchen möchte.
1) Ja. Mit Werten in Kategorien (bzw. Klassen) wie “0-5” und “6-10” lässt sich – auch dann, wenn die Kategorien die gleiche Spannweite aufweisen – nicht mehr sinnvoll rechnen (Denn was wäre “6-10” + “0-5” – wohlgemerkt unter bewusster Setzung der Anführungszeichen?). Rechnen könnte man hier ersatzweise allenfalls mit den Klassenmitten, was aber zu erheblichen Verzerrungen führen könnte. Was aber durchaus möglich wäre, ist die Bildung von Reihenfolgen (Ein Befragter der Altersgruppe “21-30” ist älter als ein Befragter der Altersgruppe “11-20”) sowie die Erfassung von Häufigkeiten (Die meisten Befragten gehörten der Altersgruppe “11-20” an). Derartig kategorisierte Daten vereinen damit alle Eigenschaften ordinal skalierter Daten auf sich. Sofern man noch über die ursprünglichen Daten verfügt, wäre eine Re-Transformation in metrische Werte durch Auflösung der Kategorien ja aber jederzeit möglich.
2) Jein. Sofern die Kategorien wie im benannten Beispiel 0=0, 1=1, 2=2 etc. lauten, ist noch keine Transformation in ordinal skalierte Daten erfolgt. In dem Moment, in dem die Kategorie >5=6 gebildet wird, dagegen schon.
Hallo Christian,
Bei einer Umfrage einer Projektarbeit haben wir nach der Mehrzahlungsbereitschaft der Teilnehmer gefragt. Als Auswahlmöglichkeit gab es die Antwortmöglichkeiten “0%”, “<15%", "<30%","50%”. Jetzt wollen wir eigentlich mittels verschiedener Regressionsanalysen den Einfluss verschiedener Merkmale wie Alter, Geschlecht, Studiengang, Persönlichkeitsmerkmale (UV) auf die Zahlungsbereitschaft (AV) ermitteln. Da es sich aber unserer Meinung nach ja ähnlich wie bei den Altersgruppen”20-30 Jahre” etc. auch um ordinalskalierte und nicht um metrische Daten handeln sollte sind wir uns nicht sicher wie wir nun fortschreiten sollten bzw. welches Regressionsmodell überhaupt geeignet ist.
Eine Überlegung wäre es die Skala im Nachhinein anzupassen. Also konkret von 0%, 15%, 30% und 45% und nicht mehr von Bereichen zu reden und die Teilnehmer aus <50% und 50% zu den 45% zuzuordnen. So sollte es ja eigentlich ein metrisches Skalenniveau darstellen. Das wäre zwar nicht sehr schön, aber da wir nicht wissen wie wir das sonst lösen sollen unser letzter Ausweg. In einem vorherigen Kommentar hast du von einer Re-Transformation geredet. Hast du da vielleicht noch mehr Informationen zu oder eventuell einen anderen Vorschlag? Eventuell können wir ja auch die Antwortmöglichkeiten beibehalten und stehen nur auf dem Schlauch was das Regressionsmodell angeht.
Vielen Dank schon einmal für deine Hilfe!
P.S: Wir haben nicht sonderlich viel Ahnung von Statistik, eigentlich sollte die ganze Umfrage auch nur deskriptiv ausgewertet werden, jedoch ist jetzt der Wunsch seitens des Betreuers aufgekommen das ganze doch etwas detaillierter zu betrachten.
@Roman Martin:
Vielen Dank für die Frage, die ich gerne bestmöglich beantworten möchte – auch wenn ich befürchte, dass ich euch mit der Antwort nicht viel Freude machen werde…
Zunächst einmal sind Prozentwerte natürlich (ebenso wie Jahreszahlen) metrisch skaliert – allerdings habt ihr sie künstlich in Klassen aufgeteilt, die (was bei der Klassierung von Daten immer schlecht ist) aber nicht gleich breit sind (1%, 15%, 15%, 20%…). Infolge dessen liegen euch nun Daten vor, mit denen man rechnerisch eher wenig anfangen kann. Warum es nicht sinnvoll sein kann, allen Elementen in einer Klasse (z.B. der Klasse 1%-14%) den oberen Grenzwert dieser Klasse (14%) zuzuweisen, liegt auf der Hand: Hätten hier fünf Personen geantwortet, hätten vielleicht zwei bei 3%, einer bei 4%, einer bei 8% und einer bei 10% gelegen – durch eine Anhebung aller Werte auf 14% würde sich in einem solchen Fall eine ganz erhebliche Verzerrung ergeben. Besser rechnen ließe sich (unter der ebenfalls kippeligen Annahme relativer Gleichverteilung innerhalb der Klassen) zwar gegebenenfalls mit den Klassenmitten (untere Klassengrenze + obere Klassengrenze -> Ergebnis durch 2 teilen), aber auch hier sorgen die abweichenden Klassenbreiten für Probleme hinsichtlich der Vergleichbarkeit.
Als Basis für eine Regressionsanalyse sind die erhobenen Daten daher meiner Einschätzung nach leider gänzlich ungeeignet – hier lässt sich bedauerlicherweise auch durch eine Transformation nichts mehr retten. Was ich aber – in Unkenntnis der Erhebungsdetails – für anwendbar halte, ist der Chi-Quadrat-Test auf stochastische Unabhängigkeit. Vielleicht könntet ihr euren Betreuer damit ja besänftigen…
https://wissenschafts-thurm.de/grundlagen-der-statistik-der-chi-quadrat-unabhaengigkeitstest/
Hallo Christian,
ich hätte auch eine Frage. Ich habe Daten mittels eines psychologischen Fragebogens erhoben und möchte berechnen ob die beiden Variablen (Alter und Geschlecht) einen Einfluss auf das Vorliegen einer depressiven Symptomatik haben. Das Alter sollte laut der Hypothese in zwei Stufen unterteilt sein (17-30 & 31-63). Die Aufteilung ergibt sich aus den realen Alterswerten der Teilnehmer was wahrscheinlich sehr willkürlich ist. Kann ich damit trotzdem rechnen und die Variable Alter dummykodieren in 0=”17-30″ und 1=”31-63″ ? Oder macht ist es sinnvoller mit den realen Werten zu rechnen und bei der Auswertung eine augenscheinliche Unterteilung vorzunehmen? Das gleiche gilt auch für die Werte der AV (Depressionswert) ich könnte die Werte in drei Kategorien aufteilen (unauffällig, mittelmäßig auffällig, klinisch auffällig) oder eben mit den realen Punktwerten des Fragebogens rechnen. Mein statistisches Wissen ist leider zu begrenzt um beurteilen zu können ob und wie es einen Sinn macht mit den Daten zu rechnen ohne völlig unnützes Zeug zu berechnen. Vielleicht hast du ja einen Tipp für mich, ich wäre dir auf jeden Fall sehr dankbar für ein kurzes Feedback.
Vielen Dank im Voraus!
Liebe Grüße
Kim
@Kim: Vielen Dank für die spannende Frage, die ich ohne detaillierte Kenntnis der Erhebung (Wie sind die Daten zustandegekommen? Welche Forschungsfragen sollen beantwortet werden? Welche statistischen Tests sollen zum Einsatz kommen und welche Kennzahlen sind zu berechnen?) leider nur unzureichend beantworten kann. Grundsätzlich würde ich aber sagen, dass man mit den realen und unklassierten Werten rechnen sollte, wenn diese vorliegen. Eine Klassierung kann allerdings dennoch – z.B. in Vorbereitung der Durchführung eines Chi²-Anpassungstests – sinnvoll sein. Falls Interesse besteht, können wir das sehr gerne per E-Mail im Detail besprechen: creinboth@hs-harz.de.
Pingback: Ein Blasendiagramm / Bubble Chart mit Nominal-Skala in Excel – nicky reinert
Vielen Dank für die interessanten Erläuterungen!
Ich habe eine konkrete Frage: Im Rahmen einer Analyse möchten wir die Wohnqualität unterschiedlicher Siedlungen vergleichen. Dazu haben wir die betrachteten Siedlungen in unterschiedliche Teilräume unterteilt und diesen Teilräumen jeweils eine Qualitätsstufe auf einer fünfstufigen Skala zugeordnet. Nun möchten wir für jede der betrachteten Siedlungen eine “Gesamtqualität” ermitteln, um die Siedlungen miteinander vergleichen zu können. Unser Gedanke war es, dazu jeweils die Flächenanteile aller Teilräume gleicher Qualitätsstufe innerhalb einer Siedlung zu ermitteln und mit dem jeweiligen Skalenwert (1 bis 5) zu multiplizieren. Dieser Schritt würde entsprechend für jede der fünf Qualitätsstufen erfolgen und anschließend würden die fünf Werte zu einem “Gesamtqualitätswert” der Siedlung aufaddiert.
Nach Ihren Erläuterungen ist dieses Verfahren aber offenbar nicht zulässig, da es sich bei den Qualitätsstufen ja um ordinalskalierte Daten handelt, die nicht “normal” verrechnet werden dürfen (so wie dies auch bei Ihrem Beispiel zu den Schulnoten der Fall ist).
Wie könnten/müssten wir stattdessen vorgehen, um die betrachteten Siedlungen miteinander vergleichen bzw. in eine Rangfolge bringen zu können?
@Jan: Vielen Dank für die interessante Frage – das hört sich nach einem durchaus spannenden Projekt an. Spräche denn grundsätzlich etwas dagegen, anstelle des arithmetischen Mittels den Median zu verwenden und die Ergebnisse nach Flächengröße zu gewichten?
Hallo Christian,
ich habe auch eine Frage. Bin mit etwas unsicher mit den Skalenniveaus. Innerhalb meines Fragebogens zur Erforschung der Wirkung von Online-Rezensionen sollen die Teilnehmer einmal einstufen ob es sich bei einer gezeigten Online-Rezension um eine “kurze” oder “lange” Bewertung handelt. Ich würde hier das “nominale Skalenniveau” wählen. Ordnen kann man die zwei ja nicht wirklich oder?
Ebenso soll eingeschätzt werden, ob die Online-Rezension “sehr positiv”, “positiv”, … oder “sehr negativ” ist (insgesamt 5 Abstufungen”). Hierbei handelt es sich dann doch um eine ordinale Skala oder?
@Jaqueline: Vielen Dank für die spannende Frage – die Antwort lautet “jein” und “ja”. Bei “kurz” und “lang” würde ich ad hoc ebenfalls von einer nominalskalierten Variable ausgehen. Man könnte aber durchaus auch argumentieren, dass eine Variable mit den Ausprägungen “sehr lang”, “lang”, “kurz” und “äußerst kurz” ja definitiv ordinal skaliert wäre und es daher auch eine auf “lang” und “kurz” verkürzte Skala sein sollte. “Lang” ist immerhin länger als “kurz”, insofern ist eine natürliche Reihenfolge erkennbar. Schwierig – ich halte beides für begründbar. Einfacher verhält es sich mit “sehr positiv”, “positiv” etc. – diese Skala ist in der Tat eindeutig ordinal.
Hallo Christian
Vielen Dank für die interessanten Ausführungen.
Ich helfe meinem Patensohn bei der Auswertung eines Experiments, das er für seine Maturaarbeit durchgeführt hat, ohne vorher genügend Beratung erhalten zu haben.
Er untersucht die Wirkung von Musik und Motivational Speech auf die Laufleistung von MItschülern (gemessen in Metern).
Drei Gruppen: Kontrolle, Musik, Speech.
Alle liefen einen Prä-Test-Lauf. Beim Post-Test-Lauf (Kontrolle wie beim Prä-Test, die anderen mit Musik oder Motivational Speech, je nach Gruppenzuteilung).
Daneben stellte er den Probanden mehrere Fragen (tw. gruppenspezifisch), alle mit demselben Aufbau. Z.B. Denkst du, dass dich die Musik hat schneller rennen lassen? Antwortmöglichkeiten von 1 bis 5, wobei nur die Ankerpunkte benannt wurden: “Ich glaube, sie machte mich viel langsamer / Ich glaube, sie machte mich viel schneller. Oder es wurde gefragt, wie gut die Musik gefallen hat. Der allergrösste Teil der Probanden kreuzten, wie vorgesehen, nur die Kästchen mit den ganzen Zahlen von 1 bis 5 an. Wenige machten in der Mitte zwischen zwei Zahlen ein Kreuz.
Hauptfragestellung ist, welche Intervention stärker ist, gemessen an der Streckendifferenz von Prä- und Posttest.
Untersucht werden soll zusätzlich aber sowohl der Einfluss auf die Streckendifferenz als auch allfällig vorhandene gegenseitige Abhängigkeit der im Fragebogen erhobenen Variablen. Beim Frageobogen handelte es sich nicht um ein validiertes Instrument, sondern um “frei formulierte Fragen”.
Die Fragen mit den Antwortmöglichkeiten von 1-5: Ist dies Quantitativ diskret (“rechenbar”) oder ordinal?. Falls ordinal: äquidistand oder nicht äquidistant?
Wie soll mit den wenigen “nicht-ganzzahligen” Antworten verfahren werden?
Welche Korrelationsmethode darf bei den Fragebogenfragen gegenseitig verwendet werden? (Pearson, Spearman oder Kendall?)
Welche Regressionsmethode darf angewendet werden? (Die Fragebogenfragen könnten neben der Intervention evtl. als weitere erklärende Variablen für die Streckendifferenz im Modell gelten.)
Ich bin sehr gespannt. (Und muss die Antwort dann auch noch in R umsetzen, das ich selber erst am lernen bin, da ich keinen Zugang mehr zu SPSS habe.
Vielen Dank im Voraus!
Ernst
@Ernst: Vielen Dank für die interessante Frage, die ich aufgrund längerer Abwesenheit leider erst verspätet (vermutlich zu spät – mea culpa) beantworten kann. Zu Ihrer Frage daher kurz einige zusammenfassende Anmerkungen (bei Interesse gerne ausführlicher):
1) Interessantes Thema, gutes Set-Up (mir Prä/Post und Kontrollgruppe!)
2) Für die Probanden muss klar erkennbar sein, ob sie bei einer Skala nur die Skalenpunkte ankreuzen, oder ihre Kreuze auch zwischen die Skalenpunkte setzen können. Wenn ein Teil der Probanden bei jeder Frage nur die Skalenpunkte nutzt, während ein anderer Teil der Probanden auch in den Zwischenräumen ankreuzt, wäre zunächst sicherzustellen, ob diese Klarheit gegeben war.
3) Ohne einen diesbezüglichen Test der Skala vorgenommen zu haben, gehe ich allein auf Basis der Beschreibung der Items davon aus, dass es sich um ordinalskalierte Variablen handelt. Dass man das Kreuz auch zwischen die Skalenpunkte hätte setzen können, macht die Skala noch nicht unbedingt zu einer äquidistanten Skala, da die wahrgenommenen Abstände zwischen den einzelnen Items trotzdem voneinander abweichen können. In diesem Fall wären Spearman oder Kendall die Korrelationskoeffizienten der Wahl.
4) Problematisch ist in diesem Fall der Umgang mit den wenigen “Zwischenwerten”. Vielleicht kann man diese jeweils als Mittelwert der beiden umschließenden Skalenpunkte in den Datensatz aufnehmen oder als fehlende Werte kennzeichnen? Um hierzu (und eigentlich auch zu den anderen Fragen) eine fundierte Auskunft geben zu können, müsste ich vorab einen Blick auf den Fragebogen werfen, den Sie mir aber sehr gerne jederzeit per E-Mail zukommen lassen können.
5) Ob eine Regressionsanalyse geeignet ist, hängt letztendlich davon ab, ob ein linearer Zusammenhang zwischen dem motivierenden Faktor und dem Ergebnis zu vermuten ist. Ist das denn hier der Fall – und falls ja, warum?
6) R ist ein großartiges Tool – wenn man den Umgang mit SPSS gewohnt ist und nicht ganz auf den Komfort (der ja aber auch ein wenig einengt) einer fertigen Statistiklösung verzichten möchte, findet man im Netz sehr gute und vollkommen kostenfreie Alternativen:
https://wissenschafts-thurm.de/kostenlose-alternativen-zu-spss-fuer-studierende-was-koennen-past-pspp-co/
Viele Grüße und viel Erfolg bei der weiteren Datenauswertung!
Christian
Guten Tag,
danke für den Artikel und die hilfreichen Kommentare. Ich hätte ebenfalls eine Frage zu Messniveaus: ich habe kognitive Tests mit Personen durchgeführt, also bestimmte Fähigkeiten getestet (z.B. Visuelles Erkennen oder räumliches Denken, wie bei einem IQ-Test). All diese Testbögen werden am Ende anhand der Punktzahl ausgewertet, die der Teilnehmer erreicht hat (z.B. 15/20 Punkten). Nun meine Frage: sind diese Werte ordinal oder metrisch zu bewerten? Ich habe bereits gesehen, dass bei Fragebögen (z.B. “Wie gut fühlen Sie sich heute auf einer Skala von 1-10?”) als ordinal zu bewerten sind. Meiner Auffassung nach wäre die Anzahl von richtigen Antworten bei einem Test aber metrisch, da 5 richtige Antworten halb so viele sind wie 10. Liege ich damit richtig?
Und wie verhält es sich, wenn ich einen Fragebogen habe, auf dem nur mit “ja” und “nein” geantwortet werden kann- ist die Anzahl von “Ja’s” als Endpunkt dann metrisch oder nominal skaliert?
Über eine Antwort würde ich mich sehr freuen.
Der Auffassung, dass ein Anteilswert (also z.B. 60% aller möglichen Punkte wurden erreicht) als metrisch zu werten ist, schließe ich mich grundsätzlich an. Ob die Berechnung metrischer Kennzahlen in diesem Fall sinnvoll ist, hängt allerdings auch von den Items selbst ab. Haben alle zu beantwortenden Fragen die gleiche Wertigkeit, wäre z.B. die Berechnung des arithmetischen Mittels gerechtfertigt, unterscheiden sie sich jedoch stark z.B. mit Blick auf ihren Schwierigkeitsgrad oder ihre Aussagekraft, wäre dies nicht der Fall. Zu Ihrer zweiten Frage: Bei einer reinen Ja/Nein-Variablen handelt es sich um ein sogenanntes dichotomes Merkmal, welches als nominalskaliert zu betrachten wäre.
Beste Grüße
Christian Reinboth
Sehr geehrter Herr Reinboth, ich hätte eine Frage und zwar wäre die Angabe: In einer Umfrage wurde den Befragten eine Liste mit Filmgenre (“Komödie”, “Krimi”, etc.) vorgelegt, die sie entsprechend Ihren Vorlieben auswählen (“ankreuzen”) sollten. Auf welchem Skalenniveau wurde hier gemessen? Gäbe es auch andere Möglichkeiten, die Vorlieben zu messen? Wenn ja, welche?
Vielen dank im Voraus und viele Grüße,
Nina
Bei Filmgenres handelt es sich eindeutig um nominalskalierte Angaben: Sie lassen sich in keine natürliche Reihenfolge bringen (also kein “Krimi steht immer vor SciFi”), feststellbar sind lediglich Gleichheit oder Ungleichheit (d.h. “diese beiden Filme gehören dem gleichen Genre an”). Abfragen könnte man solche Vorlieben neben einer einfachen Ankreuzliste z.B. auch über eine Skala, bei der sich die Probandinnen und Probanden jeweils zwischen zwei Genres entscheiden müssten (“Was würden Sie lieber sehen: Krimi oder Komödie?”) oder eine Präferenzrangfolge (“Bringen Sie diese zehn Filmgenres in die von Ihnen bevorzugte Reihenfolge, angefangen mit Ihrem Lieblingsgenre.”)
Beste Grüße
Christian Reinboth
Sehr geehrter Herr Reinboth,
zunächst einmal Vielen Dank für diesen informativen Text.
Mir ist jedoch nicht klar warum ich nicht den Zusammenhang der Absatzmenge auf den Preis (Absatzmenge; unabhängig / Preis; abhängig) überprüfen kann? Es wäre doch durchaus sinnvoll zu überprüfen, ob die Absatzmenge einen Einfluss auf den Preis hat und inwieweit diese Daten korrelieren?
Über eine kurze Rückmeldung würde ich mich sehr freuen.
MFG
Nils Ende
Sehr geehrter Herr Ende,
vielen Dank für Ihren freundlichen Kommentar sowie für Ihre Frage zur Untersuchung von Zusammenhängen bzw. Korrelationen. Leider habe ich nicht verstanden, welchem Textteil Sie entnommen haben, dass die Bestimmung einer Korrelation z.B. zwischen Absatzmenge und Preis nicht möglich sein soll – können Sie mir hier weiterhelfen? Zu beachten wäre natürlich immer, dass eine (auch starke) Korrelation kein sicherer Hinweis auf eine Kausalität im Sinne eines inhaltlichen Zusammenhangs ist, siehe hierzu z.B.:
https://wissenschafts-thurm.de/grundlagen-der-statistik-korrelation-ist-nicht-kausalitaet/
Bei Absatzmenge und Preis würde ich zudem vom Vorliegen einer beidseitigen Korrelation (d.h. Absatzmenge beeinflusst Preis und Preis beeinflusst Absatzmenge) bzw. einer sogenannten Interdependenz ausgehen, die mit besonderer Umsicht zu interpretieren wäre.
Freundliche Grüße
Christian Reinboth
Sehr geehrter Herr Reinboth,
vielen Dank für diesen informativen Text. Dieser ist äußert hilfreich!
Derzeit führe ich eine Empirische Forschung durch und habe nun bei der Auswertung der Ergebnisse Schwierigkeiten. Es sind drei Fragebögen auszuwerten.
Fragebogen 1 konnte mit den Antwortmöglichkeiten “Richtig” oder “Falsch” beantwortet werden.
Beispiel-Aussage aus Fragebogen 1:
Vor einer Wahl informiere ich mich gründlich über die Eignung der verschiedenen Kandidaten.
Fragebogen 2 konnte mit den Antwortmöglichkeiten “Ja” oder “Nein” beantwortet werden.
Beispiel-Frage aus Fragebogen 2:
Gehen Sie online, obwohl Sie Wichtigeres zu tun haben?
Fragebogen 3 konnte durch das Ankreuzen auf einer Skala von 1 bis 5 beantwortet werden.
Beispiel-Aussage aus Fragebogen 3:
Ich versuche extreme Standpunkte zu vermeiden.
Sind Fragebogen 1 und 2 nominal skaliert?
Ist Fragebogen 3 ordinal skaliert?
Oder irre ich mich?
Über eine Antwort würde ich mich sehr freuen.
Vielen Dank!
Mit freundlichen Grüßen
C. Ott
@C. Ott: Vielen Dank für den freundlichen Kommentar und natürlich für die interessante Frage. Ich kann Ihnen in allen Punkten nur Recht geben: Variablen mit den Antwortmöglichkeiten Ja/Nein oder Richtig/Falsch sind nominal skaliert, eine Variable mit Ausprägungen auf einer (Likert-)Skala von 1 bis 5 (z.B. von “sehr wichtig” bis “überhaupt nicht wichtig”) ist ordinal skaliert.
Sehr geehrter Herr Reinboth,
super und anschaulich erklärter Text zu Skalenniveaus!
Eine Frage zu den Schulnoten – welches Streuungsmaß ist für Schulnoten geeignet? Bei metrisch skalierten Daten stelle ich meistens den Mittelwert +/- Standardabweichung dar. Gibt es ein Äquivalent für die Standardabweichung beim Median? Gibt es noch ein anderes anwendbares Streuungsmaß als der Interquartilsabstand?
Über eine Antwort würde ich mich sehr freuen.
Vielen Dank im Vorab,
MFG,
Simone
@Simone: Vielen Dank für den freundlichen Kommentar. Für Schulnoten kommt in der Tat eigentlich nur der Interquartilsabstand in Frage. Vielleicht auch noch die Spannweite, auch wenn man diese mit ordinal skalierten Daten streng genommen auch nicht berechnen dürfte (und der Informationswert mutmaßlich eher gering ist, da die Spannweite im Vergleich verschiedener Klassen oder Jahre bei mindestens einer sehr guten und einer wirklich schlechten Arbeit in der Gesamtmenge ja immer gleich bliebe…). Insofern würde ich eher den IQR empfehlen.
Hallo Herr Reinboth,
Vielen Dank für diesen tollen Beitrag.
Ich habe eine Frage zu den Skalenniveaus und Tests.
Wenn ich eine metrische Variable und eine ordinal oder nominal Variable miteinander testen möchte muss ich dann immer auf dem niedrigeren Niveau testen?
Ich möchte zum Beispiel die Konzentrationsleistung anhand einer 7 stufigen Likert Skala erheben und folgend wissen, ob das Geschlecht, Alter, Einkommen oder Nationalität einen Einfluss darauf hat.
Vielen Dank für Ihre Mühe.
Liebe Grüße
Cleo Masius
@Cleo Masius: Vielen Dank für Ihre Frage!
Sie haben Recht: Wenn ein bivariater Test ein bestimmtes Mindestskalenniveau fordert, wird das (es sei denn, es ist explizit anders definiert) immer für beide Variablen gelten. Sie müssen sich bei der Frage, welche Testverfahren Sie auf Ihre Daten anwenden können, also in der Tat am niedrigsten Skalenniveau orientieren. Für das von Ihnen skizzierte Szenario könnte es sich in Abhängigkeit vom Stichprobenumfang beispielsweise lohnen, die auf der Likert-Skala abgefragten Daten zu gruppieren (z.B. in positiv, neutral, negativ) und einen Chi-Quadrat-Test auf stochastische Unabhängigkeit durchzuführen.
Weitere Informationen zu diesem Test finden Sie z.B. hier:
https://wissenschafts-thurm.de/grundlagen-der-statistik-der-chi-quadrat-unabhaengigkeitstest/
Lieber Herr Reinboth,
vielen Dank für diesen sehr informativen Artikel. Falls Sie hier noch hereinschauen, würde ich mich freuen, wenn Sie mir einen Tipp zur Codierung meiner Daten geben könnten. Ich untersuche den Einfluss verschiedener Parameter auf das wahrgenommene Alter einer Stimme. Dabei bin ich mir unsicher, welchen Datentyp ich für meine abhängige Variable “geschätztes Alter” annehmen sollte. Den Probanden wurde für jede zu beurteilende Stimme eine Skala von 10 – 90 Jahren in 5-Jahres-Abstufungen vorgegeben; d.h. es konnten nur 10, 15, 20…. usw. ausgewählt werden und keine Zwischenwerte. Macht es aus Ihrer Sicht Sinn, diese Daten als kardinalskaliert zu behandeln (und z.B. eine “normale” Regression zu rechnen), oder wäre eine Umkodierung in Altersgruppen und die Wahl eines Verfahrens für ordinalskalierte Daten sinnvoller? Nach meinem Verständnis wären vorgegebene Altersklassen wie “20 – 25” oder “25 – 30” auf jeden Fall ordinalskaliert. Da in meinem Fall aber nicht direkt Klassen vorgegeben wurden, bin ich mir unsicher, um welchen Datentyp es sich handelt.
Vielen Dank im Voraus für Ihr Feedback!
@Linguistin: Vielen Dank für die spannende Frage. Meine ad hoc-Empfehlung wäre, die Daten als ordinalskaliert zu betrachten. Grundsätzlich sind zwar alle Eigenschaften metrischer Daten gegeben (man kann Gleichheit oder Ungleichheit feststellen, man kann eine natürliche Reihenfolge bilden und man kann mit den Abständen rechnen), in der Realität beträgt der Altersabstand einer Person, die auf 50 Jahre geschätzt wurde, von einer Person, die auf 40 Jahre geschätzt wurde, ja aber nicht geschätzte 10 Jahre, weil die Probandinnen und Probanden ja die Einzelaltersangaben, nicht aber die Abstände schätzen mussten.
Den geschätzten Altersabstand würde man dagegen erhalten, wenn man den Probandinnen und Probanden jeweils zwei Testpersonen vorführen und darum bitten würde, den Altersabstand zu schätzen – und dabei müssten im obigen Beispielfall längst nicht wieder zehn Jahre herauskommen, weil die Aufgabe schlicht eine andere wäre (Wie alt ist diese Person? vs. Wie viele Jahre liegen diese Personen auseinander?). Dieser Umstand würde mich dazu bewegen zu vermuten, dass man mit den Abständen zwischen den geschätzten Altersangaben doch besser nicht rechnen sollte – und wenn das nicht geht, handelt es sich um ordinalskalierte Daten.
Ich bin mir aber sicher, dass es in diesem Fall auch abweichende Meinungen gäbe. Wie geschrieben – eine spannende Fragestellung. Was aber selbst bei Unsicherheit für die Bewertung als ordinalskaliert spricht: Die sich hieraus ergebenden Schlüsse wären in keinem Fall falsch, da alle für ordinalskalierte Daten freigegebenen Verfahren mit metrischen Daten ja ebenso nutzbar sind. Umgekehrt wäre aber die Anwendung von metrische Daten voraussetzenden Verfahren auf Daten, die sich bei näherer Betrachtung doch als ordinalskaliert erweisen, im Ergebnis fehlerbehaftet.
Ganz herzlichen Dank für die schnelle und ausführliche Antwort; das hilft mir sehr weiter!
World’s Best Neck Massager Get it Now 50% OFF + Free Shipping!
Wellness Enthusiasts! There has never been a better time to take care of your neck pain!
Our clinical-grade TENS technology will ensure you have neck relief in as little as 20 minutes.
Get Yours: hineck.online
Thank You,
Maricela
Wissenschafts-Thurm – Clevere Aussichten
Hallo Christian,
danke für den aufschlussreichen Artikel. Ich habe auch eine Frage:
Für meine Masterarbeit habe ich mehrere Variablen definiert, deren Ausprägung ich über eine Verrechnung mehrerer, unterschiedlich skalierter Ausgangsvariablen berechne. Bspw: Grad der Klimafreundlichkeit (KF) des typischen Mobilitätsverhaltens einer Person.
Der KF berechnet sich dabei über eine Funktion aus folgenden Ausgangsvariablen:
– a) typischerweise verwendetes Verkehrsmittel auf den Wegen zu verschiedenen Aktivitäten; zB auf dem Weg zur Arbeit, zum Einkaufen… die wählbaren Antwortoptionen sind hier kategorial (“PKW”, “Fahrrad”, “ÖPNV”, etc.). Je nach angegebenem Verkehrsmittel wurden die Wege nachträglich dichotomisiert (“klimafreundlich” / “nicht klimafreundlich”). Ich gehe also von einer Nominalskala bei dieser Ausgangsvariablen aus.
– b) Häufigkeit der jeweiligen Wege / Woche; Antwortoptionen auf einer Ordinalskala (z. B. “1 Mal”, “2 Mal”, “3 Mal oder häufiger”). Aufgrund der letzten Antwortoption, die ja einen unklaren Wertebereich umfasst, ist diese Variable leider nicht intervallskaliert.
– c) Distanz pro Weg in Kilometern -> Antwortoptionen auf einer Ordinalskala (z. B. “10-15 km”, “20 km oder mehr”)
Daraus habe ich den Grad der KF für jede befragte Person berechnet, indem ich den prozentualen Anteil aller Wege berechnet habe, den eine Person üblicherweise mit klimafreundlichen Verkehrsmitteln zurücklegt.
Nun ist meine Frage: Ist der Grad der KF ordinalskaliert, obwohl in seine Berechnung eine dichotomisierte Variable (Weg “klimafreundlich” oder “nicht klimafreundlich”) eingeht? Mein Gefühl sagt mir: ja. Denn ich kann die KF der Befragten ja in eine Rangfolge bringen, indem ich sage: Person A (KF = 0,50) bewegt sich gewöhnlich klimafreundlicher fort als Person B (KF = 0,25).
Oder ist der Grad der KF evtl. sogar intervallskaliert (“Person A bewegt sich gewöhnlich doppelt so klimafreundlich zurück wie Person B”)? Ich bezweifle das, aber bin mir nicht ganz sicher.
Generell gefragt: Hängt die Bestimmung des Skalenniveaus einer Variablen, die man aus mehreren, verschieden skalierten Ausgangsvariablen berechnet hat, direkt davon ab, welches das geringste Skalenniveau der Ausgangsvariablen war, oder kann die berechnete Variable ein höheres Skalenniveau aufweisen als einzelne Ausgangsvariablen?
Über deine Hilfe würde ich mich sehr freuen! Liebe Grüße!
@Anna: Vielen Dank für den Kommentar und die interessante Frage. Ich kann hier auch nur mein Bauchgefühl wiedergeben, bin aber geneigt, Deiner Einschätzung zuszustimmen. Zwar geht auch eine nominalskalierte Variable in die Berechnung ein, am Ende ist das Ergebnis ja aber ein Anteilswert, der mit einem anderen Anteilswert direkt verglichen werden kann (Person X legt 20% der km klimafreundlich zurück, Person Y dagegen 40%). Quantifizieren (Person Y legt doppelt so viele km klimafreundlich zurück wie Person X) würde ich dagegen nicht, da die zugrundeliegende km-Angabe ja ganz erheblich variieren kann. Überhaupt scheint mir da das grundsätzliche Problem mit diesem Indikator zu liegen. Ein aus der Luft gegriffenes Beispiel:
1) Person A: Fährt 200 km mit dem Auto und 400 km mit der Bahn. KF = 0,67
2) Person B: Fährt 40 km mit dem Auto und geht 40 km zu Fuß. KF = 0,50
Person A würde sich in diesem Fall klimafreundlicher fortbewegen, obwohl sie fünf mal mehr km mit dem Auto zurücklegt als Person B – es scheint mir problematisch zu sein, wenn das nicht in die Bewertung einfließt (Ggf. über die Anpassung an Durchschnitts-km pro zurückgelegtem Wegstreckentyp?). Natürlich könnte es sich bei Person A auch um einen Hausarzt handeln, der mit dem Auto Patientenbesuche druchführt, während Person B ziellos zum Spaß durch die Gegend fährt – auch das müsste ja eigentlich in die Bewertung einfließen… Spannendes Thema – schwierige Aufstellung geeigneter Variablen. Falls Du auf Twitter aktiv bist, würde ich mich in der Frage der Erfassung des persönlichen klimafreundlichen Mobilitätsverhaltens in einer einzigen, geeigneten und idealerweise auch noch metrisch skalierten Variablen mal an Katja Diehl (@kkklawitter) wenden…
Hallo Christian,
vielen Dank für deinen anschaulichen Artikel. Mir stellt sich bei meinen Daten noch eine Frage bezüglich des Skalenniveaus. Ich habe Frauen zu ihrem Stillverhalten nach der Geburt befragt. Es gibt einmal die Frage, ob grade überhaupt gestillt wird (ja/nein), die wäre ja nominal. Und dann gibt es noch mal Abstufungen, z.B.: “ja, ich stille ausschließlich”, “ja, ich stille und füttere zu”, “nein, ich habe abgestillt”. Hier bin ich mir unsicher, ob ich einen Test für eine Ordinal- oder Nominalskala auswählen sollte. Konkret, ob ich einen U-Test machen, oder nur eine Kreuztabelle nutzen kann. Man könnte ja durchaus argumentieren, dass es Abstufungen zwischen stillen, stillen und zufüttern und gar nicht stillen gibt, oder?
Vielen Dank schon einmal und herzliche Grüße,
Clara
@Clara: Vielen Dank für die interessante Frage. Ich kann da auch immer nur meine persönliche Meinung wiedergeben, würde in diesem Fall aber dazu tendieren, die Variable als ausschließlich nominal skaliert zu betrachten. Meiner Einschätzung nach gibt es bei “nicht stillen”, “nur stillen” und “stillen und zufüttern” keine natürliche Rangfolge, die ja für eine ordinale Skalierung vorliegen müsste – ähnlich wie man ja z.B. bei den Lernformen auch “visuelles Lernen”, “akustisches Lernen” und “visuelles und akustisches Lernen” in keine Rangfolge bringen könnte.
Hallo Christian,
ich hätte auch eine Frage. Und zwar habe ich die Wiedererkennungsleistung von 50 verschiedenen Symbolen durch eine statistische Analyse in 50 Ränge abstufen können. Rang 1 hat somit die höchste Wiedererkennungsleistung, Rang 50 die niedrigste. Diese sind somit ordinal (?) skaliert. Außerdem wollte ich den eingetragenen Abstand zum Symbol (in cm) mit diesen Rängen korrelieren lassen. Also: ob man seine Position näher an einem Symbol einträgt, wenn dieses eine höhere Wiedererkennungsleistung hat. Die Werte der Abstandspositionen haben aber keine “perfekten” Werte, wie bspw. 2 cm Entfernung, 4 cm, 6 cm etc. Dabei ist aber 1 cm Abstand besser als 5 cm usw. Somit könnte man diese Werte auch in Ränge klassifizieren.
Nun meine Frage: sind die Abstände auch ordinal skaliert?
Vielen Dank und viele Grüße
Lena
@Lena: Vielen Dank für die Frage. Ich bin mir nicht sicher, ob ich das Versuchssetting richtig verstanden habe, würde ad hoc aber sagen, dass beide Variablen ordinal skaliert sind. Sowohl bei der Wiedererkennungsleistung (besser > schlechter) als auch bei den Abständen (näher dran > weiter weg) gibt es erkennbar eine natürliche Reihenfolge der Items, allerdings scheint es mir in beiden Fällen so zu sein, dass die Abstände nicht quantifizierbar sind. Insofern würde ich beide Variablen als ordinal skaliert betrachten. Bei der späteren Auswertung (z.B. bei der Vergabe von Rängen für Rangkorrelationskoeffizienten) gilt es außerdem zu beachten, dass die Wiedererkennungswerte sich möglicherweise von klein (= niedriger Wert) auf groß (= hoher Wert) sortieren, die Abstandswerte aber ggf. von groß (= großer Abstand) auf klein (= geringer Abstand).
Hallo Christian, ich habe ebenfalls eine Frage, die mich leider bereits eine Weile beschäftigt und an der ich nicht gut weiterkomme.
Wir haben zwei Subskalen, die sich aus einmal 17 und einmal 19 Items zusammensetzen und für zwei Facetten des selben Konstrukts stehen. Die in die Skalen eingehenden vierstufigen Items sind leider nur ordinalskaliert und definitiv nicht normalverteilt (schief und teilweise zweigipflig usw.). Das ist inhaltlich von der Messung her auch durchaus so erwünscht. Es ist eine Beobachtungsskala (Erfassung von Interaktionsqualität), bei der bei jedem Item die vier Stufen anhand von beobachtbaren Indikatoren eingeschätzt werden (dichotom – Stufe erfüllt oder nicht erfüllt). Die Stufen bauen aufeinander auf, so dass die letzte erreichte Stufe den Wert des Items bildet (1, 2, 3 oder 4).
Für die Skalenbildung habe ich jeweils den Median verwendet (ich hoffe das war aufgrund des Skalenniveaus korrekt, ich werde ständig gefragt, warum ich nicht den Mittelwert nehme).
Ich möchte nun einen Ländervergleich mit zwei Stichproben in beiden Subskalen machen.
Bei metrischen, normalverteilen Daten hätte ich eine Manova gemacht, ich finde aber für dieses Verfahren irgendwie kein nonparametrisches Äquivalent.
Hättest du da eine Idee?
Herzliche Grüße und vielen Dank in Voraus, Manja
@Manja: Vielen Dank für die interessante Frage. Ich bin mir leider nicht sicher, ob ich den geschilderten Sachverhalt korrekt verstanden habe: Im Grunde handelt es sich bei den einzelnen Stufen eines Indikators um ja/nein-Stufen, die mit 0/1 codiert und anschließend zu einem Wert zwischen 1 und 4 (Warum eigentlich nicht 0 und 4?) zusammengeführt werden – richtig? Dieser Wert, der im Grunde ja ein reiner »Zähler« für die »jas« ist, wird danach als numerische Variable behandelt (Medianberechnung, Skalenbildung)? Schon da bin ich mir ad hoc unsicher. Würde man bei einer anderen dichotomen Variable (z.B. männlich/weiblich) ebenso vorgehen, wenn sie auf 0/1 codiert wäre? Vielleicht verstehe ich hier aber auch schlicht das Vorgehen falsch. Ggf. lohnt es sich, sich hierzu noch einmal per E-Mail oder in den Kommentaren im Detail auszutauschen. Bezüglich der Auswertung hätte ich bei der Menge an zu berücksichtigenden Variablen spontan ebenfalls keine gute Idee. Vielleicht eine Rangkorrelation (Spearman, Kendall) mit den Ländern als Datenreihen und den jeweils identischen Skalen als Datenpaaren?
@Christian. Vielen Dank für die schnelle Reaktion und ein großes Kompliment für die “Bespielung” dieses Blogs.
Ich versuche mal, das Vorgehen der Datengewinnung genauer zu beschreiben. Wir haben 36 Items (auf zwei Subskalen verteilt) im Wertebereich zwischen 1 und 4. (Ja, man hätte auch bei 0 beginnen können, die Zahlenbelegung ist historisch gewachsen und spielt bei Ordinal aus meiner Sicht keine Rolle, oder?)
Die Werte sind inhaltlich definiert mit 1= unzureichende Qualität, 2= minimale Qualität, 3=gute Qualität und 4= ausgezeichnete Qualität.
Zur Entscheidung, welcher Wert (1-4) für ein Item zutrifft, kommt man über die Einschätzung des Items auf den 4 Stufen. Jede Stufe hat für die Beobachtung konkrete Verhaltensmarker beschrieben, so dass der Beobachter einschätzen kann, ob das Verhalten in ausreichendem Maß für die Erfüllung der jeweiligen Stufe gesehen wurde. Die Stufen bauen aufeinander auf (die obere inkludiert immer die unteren). Der Wert 3 bedeutet also Stufen 1-3 ist erfüllt, Stufe 4 nicht mehr.
Aus den sich so ergebenden 36 Werten haben wir zwei medianbasierte Skalenscores (Lernanregung und Beziehungsförderung) gebildet und wollen nun in zwei Stichproben vergleichen, ob sich die Stichproben bezüglich der Ausprägungen der Subskalen unterscheiden.
Meine Stichprobengrößen liegen bei 123 und 127, sind also zumindest von der Größe her recht ausgewogen. Ich könnte die Frage sicher mit nonparametrischen Einzeltests angehen, muss dann aber das Fehlerniveau korrigieren. Ich hatte gehofft, dass es eine verteilungsfreie/ nonparametrische Analysemethode gibt, die der Manova entspricht, aber ich finde trotz viel Suche irgendwie nichts Gescheites dazu.
Ich hoffe, dass ich das Problem jetzt verständlicher beschrieben habe, gebe aber auch gern weitere Auskunft dazu.
Herzliche Grüße, Manja
Hi, hierzu habe ich auch eine Frage:
ich würde gerne einen t-test durchführen und herausfinden, ob sich zwei Einkommensgruppen (1. 2500) in ihrem Depressionslevel (abhängige Variabel) voneinander unterscheiden.
Für den unabhängigen t-test brauche ich ja eigentlich eine nominalskalierte Variabel. Das ist ja mit dem Einkommen nicht gegeben. Kann ich trotzdem einen t-test rechnen?
Vg, Sina
@Sina: Vielen Dank für die Frage. Falls ich sie richtig verstehe, zielt sie darauf ab, ob das Einkommen als gruppenbildende Variable geeignet ist. Das ist zunächst nicht der Fall, weil sich durch die stetige Natur der Werte viel zu viele Gruppen ergeben – oft vermutlich nur mit einem einzigen Fall. Trotzdem könnte man aus dem Einkommen durch Gruppierung (z.B. “weniger als 2.500 EUR Einkommen” oder “Einkommen von 2.500 EUR und mehr”) ja eine geeignete Variable ableiten. Oder verstehe ich die Frage falsch?
Hallo Christian,
ich stehe gerade etwas auf dem Schlauch.. vielleicht kannst du mir helfen.
Ich untersuche, ob es Korrelationen zwischen der COVID-19 Impf-Zögerlichkeit und politischem Vetrauen gibt. Die Variablen zum politischem Vertrauen sind ordinal skaliert (5-stufige Likert Skala: stimme voll zu – stimme überhaupt nicht zu) und die Variable der Impf-Zögerlichkeit stellt die Frage, ob man sich gegen das Coronavirus impfen lassen möchte.
Als Antwortmöglichkeit gibt es Nein, Weiß nicht, Ja.
Ich finde es logisch dies als ordinal zu betrachten, da eine natürliche Reihenfolge zu erkennen ist von Ablehnung über Indiffernz zu Annahme. Sehe ich das richtig?
Oder ist dies streng genommen nominal skaliert wodurch ledilich der Chi² Tets infrage käme?
Danke und lieben Gruß
Daphne
Hallo Christian,
ich untersuche, ob es Korrelationen zwischen der COVID-19 Impf-Zögerlichkeit und politischem Vertrauen gibt. Die Variablen zu politischem Vertrauen sind dabei ordinal skaliert (5-stufige Likert Skala). Bei der Variable zu Impf-Zögerlichkeit wird gefragt, ob man sich gegen das Coronavirus impfen lassen würde. Die Antwortmöglichkeiten sind (1) Nein, (2) Weiß nicht, (3) Ja.
Ich finde es logisch, dass man die Variable als ordinal skaliert einordnet, da man die Antworten in eine natürliche Reihenfolge bringen kann. Von Ablehnung über Indifferenz zu Annahme. Oder liege ich falsch und die Variable ist tatsächlich nominal skaliert?
Vielen Dank und liebe Grüße
Daphne
@Daphne: Vielen Dank für diese wirklich interessante Frage. Ich kann gut nachvollziehen, wieso man Ja/Weiß nicht/Nein als Ausdruck eines Kontinuums und damit als ordinal betrachten könnte, würde es aber dennoch als nominal einstufen. Zunächst einmal könnte man mit dieser Begründung (“Grad der Zustimmung/der Korrektheit/des Zutreffens” etc. pp.) ja absolut jede Ja/Nein-Variable als ordinal betrachten, indem man eine natürliche Rangfolge impliziert, die meinem Erachten nach aber nicht gegeben ist. Die Aussage “Ich will mich impfen lassen” könnte man ja ebenso auch als “Ich will mich nicht impfen lassen” umformulieren – schon wären “Ja” und “Nein” genau andersherum definiert und die Skala würde sich quasi umdrehen. Hinzu kommt in diesem Fall das “Weiß nicht”, das ja eine sehr breite Anzahl von Möglichkeiten – von “ich habe mich noch nicht entschieden” und “das interessiert mich gar nicht” über “ich habe mich intensiv mit dem Thema befasst und kenne die Antwort nicht” bis hin zu “ich habe mich so wenig mit dem Thema befasst, dass ich dazu keine Meinung habe” – abdeckt. All diese Spielarten von “Weiß nicht” auf einem imaginierten Kontinuum einfach zwischen “Ja” und “Nein” zu verorten, scheint mir auf jeden Fall falsch zu sein. Insofern: Interessanter Denkansatz – das wäre in einem Seminar auf jeden Fall eine Top-Frage gewesen. Ich würde dem aber klar nicht zustimmen und empfehlen, Ja/Weiß nicht/Nein als nominal zu behandeln.
Lieber Christian,
danke für die ausführliche Erklärung! Das macht Sinn
Hallo,
ich habe eine vermutlich total banale Frage aber ich fange gerade erst an mich mit Statistik zu beschäftigen. 🙂
Sehe ich es richtig, dass ein Test auf Normalverteilung erst ab metrischem Skalenniveau sinnvoll ist? Da ich ja erst dann mit Mittelwert etc. arbeiten kann.
Und hängt die Wahl meines Hypothesentests dann immer davon ab, ob die AV normalverteilt ist?
Vielen Dank schon mal vorab.
Grüße
Liane
@Liana Windisch: Vielen Dank für die Frage und viel Spaß beim Einstieg in die Statistik. Beide Fragen lassen sich bejahen: Liegen keine metrisch skalierten Daten vor, ist die Frage, ob diese normalverteilt sind, in der Tat nicht relevant. Bei metrisch skalierten Daten ist die das Vorliegen einer Normalverteilung dagegen eine der häufigsten Voraussetzungen für die Durchführung von Hypothesentests (z.B. t-Test oder ANOVA).
Lieber Christian,
vielen Dank für deine hilfreiche Einführung. Ich bin noch ganz am Anfang und habe gleich zwei Fragen an dich:
1. Bei Abfrage einer Zustimmung von Personen, z.B. “Ich kann Unterricht für heterogene Gruppen planen” (1=stimme ganz zu, 4 = stimme nicht zu), erhalte ich ordinale Skalen, wenn ich deiner Einführung richtig folge. Wenn ich nun nach einer Intervention die Fragen neu beantworten lasse und sehen möchte, ob sich die Antworten durch die Intervention ändern, müsste ich doch die Mittelwerte vergleichen und so die Veränderung sehen. Wenn ich dich jedoch richtig verstehe, darf ich bei ordinalskalierten Daten keinen Mittelwert berechnen. Wie kann ich die Veränderung berechnen? Kann ich überprüfen, ob die Veränderungen signifikant sind?
2. Welche Daten erhalte ich, wenn ich Häufigkeiten abfrage, konkret: “Inwiefern haben Sie von der Zusammenarbeit profitiert” und die Teilnehmer*innen können aus einer Reihe an Antworten auswählen (Mehrfachantworten möglich), z.B. Perspektivenwechsel, Abbau von Vorurteilen etc. Und auch hier wieder, wie kann ich die Antworten vor der Intervention mit jenen nach der Intervention vergleichen?
Vielen Dank schon vorab!
Liebe Grüße
@Claudia: Vielen Dank für die interessanten Fragen – und Entschuldigung für die verspätete Rückantwort. Dies kurz zu den weiteren Punkten:
1) Man könnte diese Information über eine validierte Skala abfragen, die Werte liefert, die als metrisch interpretiert werden dürfen, grundsätzlich sind sie aber in der Tat ordinal. Für ordinalskalierte Daten lässt sich aber trotzdem ein Mittelwert berechnen – nur eben nicht das arithmetische Mittel, welches wir manchmal als “den” Mittelwert betrachten, das aber nicht der einzige Mittelwert ist. Für ordinalskalierte Daten böte sich insbesondere der Median als Mittelwert an – und die beiden Medianwerte ließen sich dann auch miteinander vergleichen. Für die Prüfung auf eine signifikante Veränderung könnte man in diesem Fall (wenn man genügend Proband*innen hat) den Chi-Quadrat-Unabhängigkeitstest verwenden:
https://wissenschafts-thurm.de/grundlagen-der-statistik-lagemasse-median-quartile-perzentile-und-modus/
https://wissenschafts-thurm.de/grundlagen-der-statistik-der-chi-quadrat-unabhaengigkeitstest/
2) Das sind meiner Einschätzung nach nominalskalierte Daten, da sie keine natürliche Reihenfolge aufweisen (“Perspektivwechsel” steht weder “vor” noch “hinter” dem “Abbau von Vorurteilen”) und zudem ja Mehrfachantworten gegeben werden konnten. Man erhält im Grunde also eine dichotome (Ja/Nein) Variable für jede einzelne Eigenschaft. Hier könnte man zunächst einfach auszählen (“Vor der Intervention gaben XX% der Proband*innen an, dass sie sich von der Maßnahme einen Perspektivwechsel erwarten, nach der Intervention waren es XX%”) und für die Frage nach einer signifikanten Änderung ebenfalls auf den Chi-Quadrat-Unabhängigkeitstest zurückgreifen (allerdings unter Berücksichtigung der Alpha-Fehlerinflation).
Beste Grüße und maximalen Erfolg mit der Erhebung!